Calculus Second Semester: Math 3112

Problem 1. Evaluate

$$\int_{0}^{\pi/4} (2x^2 -x)\tan^{-1}(x) dx$$

and

$$\int \cos^2(x)\sin^4(x) dx$$

Problem 2. Find the limit of

(a)

$$\lim_{x \rightarrow 0} \frac{x^2- \sin^2(x)}{1 - x^2/2 - \cos(x)}$$

(b)

$$\lim_{x \rightarrow 0} \frac{x^5(e^{x^3} - 1)}{\cos(x^2) -1 - x^4/2}$$

Problem 3. Determine the convergence or divergence of

(a)

$$\int_{0}^{1} \frac{1}{\sqrt{2x-x^2}}dx$$. Find its value if it converges.

(b)

$$\int_{0}^{\pi/2} \frac{\tan(x)}{x^{3/2}+x^2}dx$$.

(c)

$$\int_{0}^{\infty} \frac{\sin(1/x)}{\sqrt{x} +x}dx$$

Problem 4. Determine whether the following series are convergent..

(d)

$$\sum_{n=1}^{\infty} \frac{(n+3)! - n!}{2^{n-1}}$$

(e)

$$\sum_{n=1}^{\infty} \frac{n^4 3^{2n+1}}{10^{n-1}}$$.

Problem 5. Find the set of convergence for

$$\sum_{n=0}^{\infty} \frac{\sqrt{n}}{n+3} x^n.$$

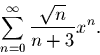
Problem 6. Let

$$f(x) = \frac{e^x}{1-x} = a_0 + a_1 x + a_2 x^2 + ......$$

Find a₀ , a₁, a₂, a₃, a₄.

Problem 7. Find f⁽⁹⁾(0) and f⁽¹⁰⁾(0), where

$$f(x) = x \ln(1 + x^3).$$

Hint: In order to find the Taylor series of $\ln(1+x)$ at 0, use the derivative technique.

Problem 8. Find the first three terms of the series for the function

$$f(x) = (1+x^2) \sqrt{1 - x},$$

at x₀ = 0.

If you would like to send me a message click Here.