RULES OF LOGARITHMS - Example

Let a be a positive number such that a does not equal 1, let n be a real number, and let u and v be positive real numbers.

Logarithmic Rule 1:

Example 3: Suppose that a base is 4 and exponents are 5, 2, and 3. We could solve the exponential problem by calculating ,

, and separately and multiplying the results. , and and their product is . You could also solve the problem by first combing the exponents

The same is true of logarithms. Suppose you wanted to calculate

. You could calculate the answer by first multiplying , changing the base of 4 to either 10 or e and calculating the results.

Or you could combine the logarithms using Rule 1 and then change the bases.

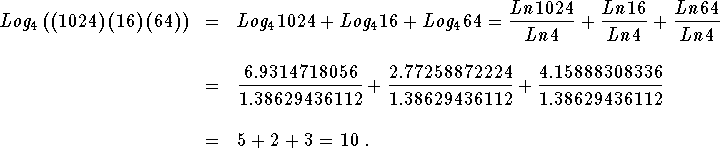
displaymath183

If you would like to review another example, click on Example.