No Title

EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS

Note:

In order to solve for x, you must isolate x.
In order to isolate x, you must remove it from under the radical.
If there is just one radical in the equation, isolate the radical.
Then raise both sides of the equation to a power equal to the index of the radical.
With these types of equations, sometimes there are extraneous solutions; therefore, you must check your answers.
If the index of the radical is even, many times there will be a restriction on the values of x.

Example 2:. $\sqrt[3]{\left( 2x-7\right) ^{2}}+3=5$

Isolate the radical term

$\begin{eqnarray*}\sqrt[3]{\left( 2x-7\right) ^{2}} &=&2 \\ && \end{eqnarray*}$

Raise both sides of the equation to the power 3 and simplify.

$\begin{eqnarray*}\left( \sqrt[3]{\left( 2x-7\right) ^{2}}\right) ^{3} &=&\left( ... ...-28x+49 &=&8 \\ && \\ && \\ 4x^{2}-28x+41 &=&0 \\ && \\ && \end{eqnarray*}$

Solve using the quadratic formula.

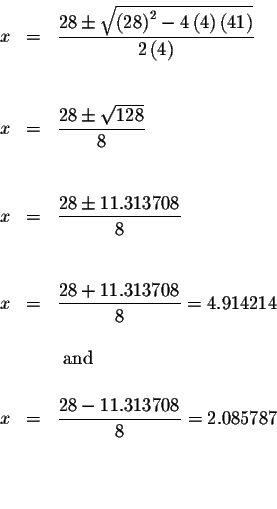
$\begin{eqnarray*}x &=&\displaystyle \frac{28\pm \sqrt{\left( 28\right) ^{2}-4\le... ...isplaystyle \frac{28-11.313708}{8}=2.085787 \\ && \\ && \\ && \end{eqnarray*}$

The answers are x=4.914214 (rounded) and x=2.085787.

Check the solution by substituting 4.914214 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

Left side: $\sqrt[3]{\left( 2\left( 4.914214\right) -7\right) ^{2}} +3=2+3=5$

Right Side: 5

Since the left side of the original equation equals the right side of the original equation after you substitute 4.914214 for x, then 4.914214 is a solution.

Check the solution by substituting 2.085787 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

Left side: $\sqrt[3]{\left( 2\left( 2.085787\right) -7\right) ^{2}} +3=2+3=5$

Right Side: 5

Since the left side of the original equation equals the right side of the original equation after you substitute 2.085787 for x, then 2.085787 is a solution.

You can also check your solution by graphing the function

$\begin{eqnarray*}f(x) &=&\sqrt[3]{\left( 2x-7\right) ^{2}}-2 \\ && \\ && \end{eqnarray*}$

The above function is formed by subtracting the right side of the original equation from the left side of the original equation. The x-intercept of the graph is the solution to the original equation. As you can see, there are two x-intercepts: 2.085787 and 4.914214. We have verified our solutions graphically.

If you would like to work another example, click on example.
If you would like to test yourself by working some problems similar to this example, click on problem.

If you would like to go back to the equation table of contents, click on contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page