No Title

EQUATIONS CONTAINING VARIABLES UNDER ONE OR MORE RADICALS

Note:

In order to solve for x, you must isolate x.
In order to isolate x, you must remove it from under the radical.
If there is just one radical in the equation, isolate the radical.
Then raise both sides of the equation to a power equal to the index of the radical.
With these types of equations, sometimes there are extraneous solutions; therefore, you must check your answers.
If the index of the radical is even, many times there will be a restriction on the values of x.

Problem2.7a $\sqrt[7]{5x+3}+\displaystyle \frac{2}{3}=\displaystyle \frac{8}{3}$

Answer: x=25

Solution:

Isolate the radical term.

$\begin{eqnarray*}&&\\ \sqrt[7]{5x+3} &=&2 \\ && \end{eqnarray*}$

Raise both sides of the equation to the 7th power.

$\begin{eqnarray*}&&\\ \left( \sqrt[7]{5x+3}\right) ^{7} &=&\left( 2\right) ^{7}... ...&128 \\ && \\ && \\ 5x &=&125 \\ && \\ && \\ x &=&25\\ && \end{eqnarray*}$

Check your answer by substituting 25 in the original equation. If the left side of the original equation equals the right side of the original equation after the substitution, the answer 25

Left Side: $\qquad \sqrt[7]{5\left( 25\right) +3}+\displaystyle \frac{2}{3}=2+\displaystyle \frac{2}{3}= \displaystyle \frac{8}{3}$

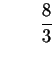
Right Side $\qquad \displaystyle \frac{8}{3}$

You can also check the answer by graphing the equation:

$\begin{eqnarray*}&&\\ y &=&\sqrt[7]{5x+3}-2 \\ && \\ && \end{eqnarray*}$

The graph represents the right side of the original equation minus the left side of the original equation.. Note that the x-intercept on the graph is located at 25, this confirms that 25 is our solution.

If you would like to go back to the problem page, click on problem.

If you would like to go back to the equation table of contents, click on contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page