SOLVING QUADRATIC EQUATIONS

Note:

• A quadratic equation is a polynomial equation of degree 2.

• The ''U'' shaped graph of a quadratic is called a parabola.

• A quadratic equation has two solutions. Either two distinct real solutions, one double real solution or two imaginary solutions.

• There are several methods you can use to solve a quadratic equation:
  1. Factoring
  2. Completing the Square
  3. Quadratic Formula
  4. Graphing

• All methods start with setting the equation equal to zero.

Solve for x in the following equation.

Example 3:

The equation is already equal to zero.

Method 1:Factoring

Since the equation is not easily factored, we will skip this method.

Method 2:Completing the square

Add 4 to both sides of the equation .

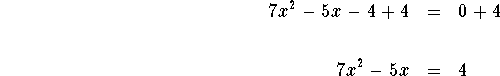
Divide both sides by 7 :

Add 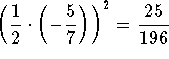to both sides of the equation :

Factor the left side and simplify the right side :

Take the square root of both sides of the equation :

Add to both sides of the equation :

Method 3:Quadratic Formula

The quadratic formula is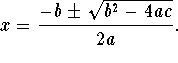

In the equation , a is the coefficient of the term, b is the coefficient of the x term, and c is the constant. Substitute 7 for a, -5 for b, and -4 for c in the quadratic formula and simplify

.

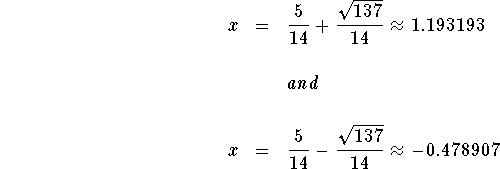
Method 4:Graphing

Graph and y=0. The graph of y=0 is nothing more than the x-axis. So what you will be looking for is where the graph of crosses the x-axis. Another way of saying this is that the x-intercepts are the solutions to this equation.

You can see from the graph that there are two x-intercepts located at 1.193193 and -0.478907. This means that there are two real answers: x=1.193193 and The answers are 1.193193 and -0.478907. These answers may or may not be solutions to the original equation. You must check the answers with the original equation.

Check these answers in the original equation.

Check the solution x=1.193193 by substituting 1.193193 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

• Right Side:

Since the left side of the original equation is equal to the right side of the original equation after we substitute the value x=1.193193 for x, then x=1.193193 is a solution.

Check the solution x=-0.478907 by substituting -0.478907 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

• Right Side:

Since the left side of the original equation is equal to the right side of the original equation after we substitute the value -0.478907 for x, then x=-0.478907 is a solution.

The solutions to the equation are - 0.478907 and 1.193193.

If you would like to work another example, click on Example.

If you would like to test yourself by working some problems similar to this example, click on Problem.

If you would like to go back to the equation table of contents, click on Contents.

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA