SOLVING QUADRATIC EQUATIONS

Note:

• A quadratic equation is a polynomial equation of degree 2.

• The ''U'' shaped graph of a quadratic is called a parabola.

• A quadratic equation has two solutions. Either two distinct real solutions, one double real solution or two imaginary solutions.

• There are several methods you can use to solve a quadratic equation :
  1. Factoring
  2. Completing the Square
  3. Quadratic Formula
  4. Graphing

• All methods start with setting the equation equal to zero.

Solve for x in the following equation.

Problem 4.3c:

Answer: 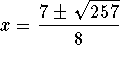exact answers;

and approximate answers

Solution:

The equation is already set to zero. Simplify the equation to .

Method 1: Factoring

The equation is not easily factored, so we will not use this method.

Method 2: Completing the square

Add 13 to both sides of the equation .

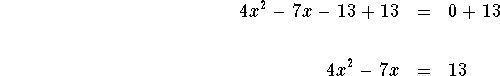
Divide both sides by 4:

Add 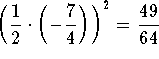to both sides of the equation:

Factor the left side and simplify the right side :

Take the square root of both sides of the equation:

Add to both sides of the equation:

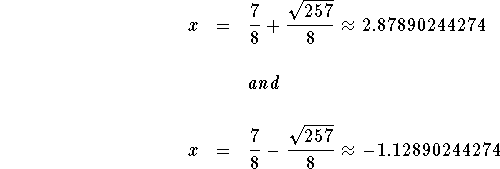
Method 3: Quadratic Formula

The quadratic formula is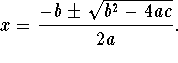

In the equation ,a is the coefficient of the term, b is the coefficient of the x term, and c is the constant. Substitute 4 for a, -7 for b, and -13 for c in the quadratic formula and simplify.

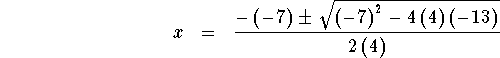
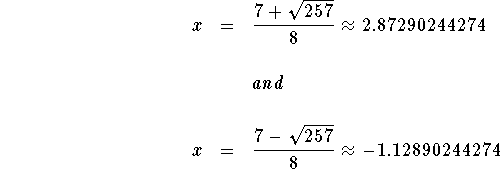
Method 4: Graphing

Graph (formed by subtracting the right side of the original equation from the left side of the original equation). Graph y=0 (the x-axis). What you will be looking for is where the graph of crosses the x-axis. Another way of saying this is that the x-intercepts are the solutions to this equation.

You can see from the graph that there are two x-intercepts located at 2.87290244274 and -1.12890244274. This means that there are two real answers: x=2.87290244274 and

The answers are 2.87290244274 and -1.12890244274. These answers may or may not be solutions to the original equation. You must check the answers with the original equation.

Check these answers in the original equation.

Check the solution x=2.87290244274 by substituting 2.87290244274 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

  
  

• Right Side:

  Left Side:

Since the left side of the original equation is equal to the right side of the original equation after we substitute the value 2.87290244274 for x, then x=2.87290244274 is a solution.

Check the solution x=-1.12890244274 by substituting -1.12890244274 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

  
  

• Right Side:

Since the left side of the original equation is equal to the right side of the original equation after we substitute the value -1.12890244274 for x, then x=-1.12890244274 is a solution.

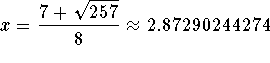The solutions to the equation are and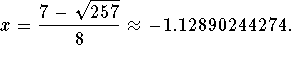

Comment: You can use the exact solutions to factor the original equation .

For example, since 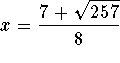, then

Since 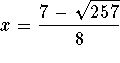, then

Since the product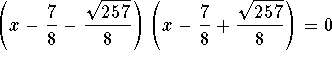

and then 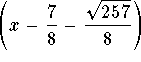and 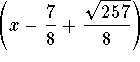are factors of

However not the only factors:

Since the first term of the product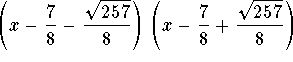

is not there must be another factor of 4:

Let s check to see whether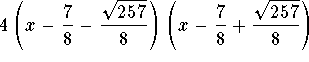

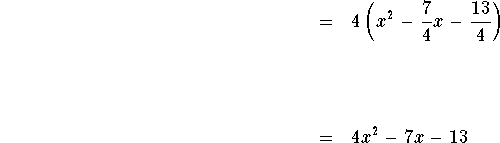
Therefore is factored as

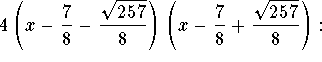
If you would like to review the solution to 4.3d, click on Problem

If you would like to go back to the problem page, click on Problem

If you would like to go back to the equation table of contents, click on Contents

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA