EQUATIONS INVOLVING FRACTIONS (RATIONAL EQUATIONS)

Note:

• A rational equation is an equation where at least one denominator contains a variable.

• There is a restriction on the domain. The variable cannot take on any number that would cause any denominator to be zero.

• The first step in solving a rational equation is to convert the equation to an equivalent equation without denominators.

• Then set the equation equal to zero and solve.

• Remember that you are trying to isolate the variable.

For an in-depth review on fractions, click on fractions

Solve for x in the following equation.

Problem 5.1e:

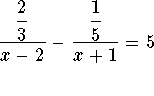
Answer:

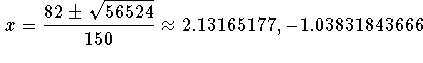
Solution:

Whenever the numerator or the denominator is itself a fraction, you have a compound fraction. The first step is to convert the compound fractions to simple fractions.

Multiply both sides of the equation by 15 so that the fractions are written as simple fractions.

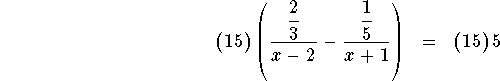
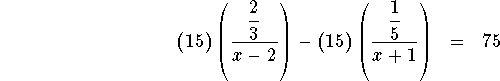
Recall that you cannot divide by zero. Therefore, the first fraction is valid if , and the second fraction is valid if If either 2 or -1 turn out to be solutions, you must discard them as extraneous solutions.

The least least common multiple (the smallest expression that all the denominators will divide into evenly) is . Multiply both sides of the equation 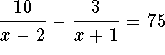by the least common multiple

which is equivalent to

which can be rewritten as

which can be rewritten as

which can be rewritten as

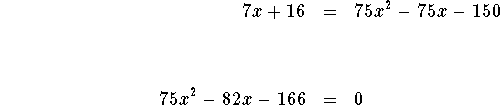
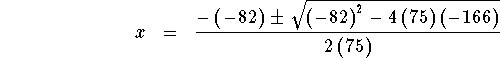
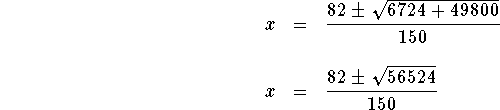
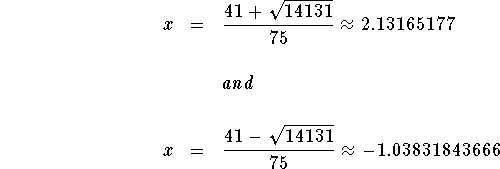
The answers are and

Check this answer in the original equation.

Check the solution x=2.13165177 by substituting 2.13165177 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

  
  

• Right Side:

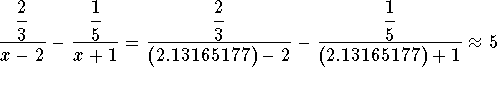
Since the left side of the original equation is equal to the right side of the original equation after we substitute the value 2.13165177 for x, then x=2.13165177 is a solution.

Check the solution x=-1.03831843666 by substituting -1.03831843666 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.

• Left Side:

• Right Side:

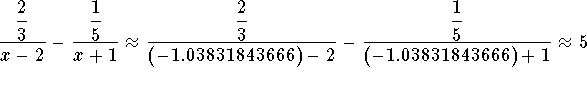
Since the left side of the original equation is equal to the right side of the original equation after we substitute the value -1.03831843666 for x, then x=-1.03831843666 is a solution.

You can also check your answer by graphing 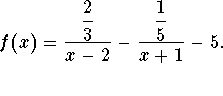(formed by subtracting the right side of the original equation from the left side). Look to see where the graph crosses the x-axis; that will be the real solution. Note that the graph crosses the x-axis at and . This means that the real solutions are and .

If you would like to test yourself by working some problems similar to this example, click on Problem

If you would like to go back to the equation table of contents, click on this example, click on Contents

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA