 EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)
EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)
 EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)
EQUATIONS INVOLVING
FRACTIONS (RATIONAL EQUATIONS)

Note:
If you would like an in-depth review of fractions, click on Fractions.
Solve for x in the following equation.
Example 1:
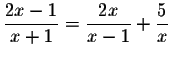
Recall that you cannot divide by zero. Therefore, the first fraction is
valid if ,
![]() the second fraction is valid if
the second fraction is valid if
![]() and the third fraction is valid if
and the third fraction is valid if![]() .If
.If ![]()
![]()
![]() turn out to be the solutions, you
must discard them as extraneous solutions.
turn out to be the solutions, you
must discard them as extraneous solutions.
The first step is always to rewrite the problem so that every denominator is
factored. In this problem, the denominator does not need factoring.
Multiply both sides of the equation by the least common multiple
![]() (the smallest
number that all the denominators will divide into evenly). This step will
eliminate all the denominators in the equation. The resulting equation may
be equivalent (same solutions as the original equation) or it may not be
equivalent (extraneous solutions),
(the smallest
number that all the denominators will divide into evenly). This step will
eliminate all the denominators in the equation. The resulting equation may
be equivalent (same solutions as the original equation) or it may not be
equivalent (extraneous solutions),
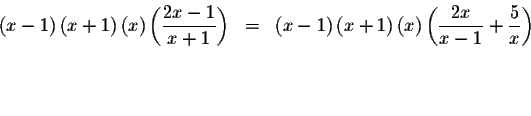
which is equivalent to
which can be rewritten as
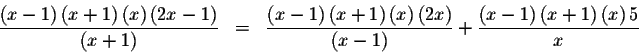
which can be rewritten again as
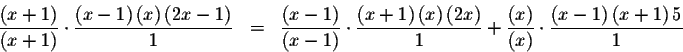
![\begin{eqnarray*}\left( x-1\right) \left( x\right) \left( 2x-1\right) &=&\left( ...
...
x+1\right) +5\left[ \left( x-1\right) \left( x+1\right) \right]
\end{eqnarray*}](img18.gif)
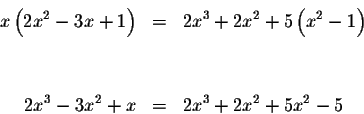
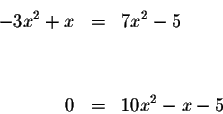
Solve for x using the quadratic formula:
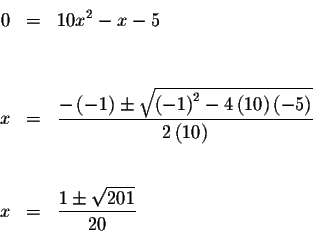
The exact answers are
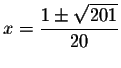 and the approximate
answers are
x=0.758872343938 and
x=-0.658872343938.
and the approximate
answers are
x=0.758872343938 and
x=-0.658872343938.
Check the answer in the original equation.
Check the solution
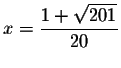 by substituting
x=0.758872343938 in the original equation for x. If the left side of the
equation equals the right side of the equation after the substitution, you
have found the correct answer.
by substituting
x=0.758872343938 in the original equation for x. If the left side of the
equation equals the right side of the equation after the substitution, you
have found the correct answer.
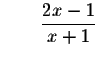
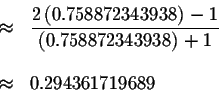
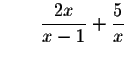
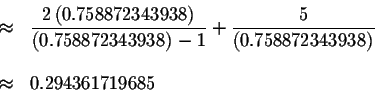
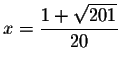 is a
solution to the original problem.
is a
solution to the original problem.
Check the solution
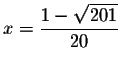 by substituting
x=-0.658872343938 in the original equation for x. If the left side of the
equation equals the right side of the equation after the substitution, you
have found the correct answer.
by substituting
x=-0.658872343938 in the original equation for x. If the left side of the
equation equals the right side of the equation after the substitution, you
have found the correct answer.
Left Side:
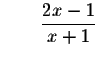
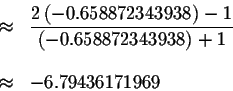
Right Side:
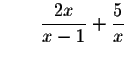
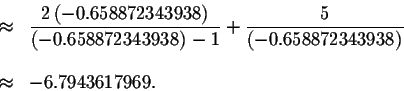
Since the left side of the original equation equals the right side of the
original equation after we substitute the value
-0.658872343938 for x, we
have verified that
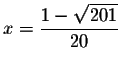 is a solution.
is a solution.
You can also check your answer by graphing
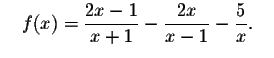 (formed by subtracting the
right side of the original equation from the left side). Look to see where
the graph crosses the x-axis; the intercept(s) will be the real solution(s).
Note that the graph crosses the x-axis in two places:
-0.658872343938 and
0.758872343938.
(formed by subtracting the
right side of the original equation from the left side). Look to see where
the graph crosses the x-axis; the intercept(s) will be the real solution(s).
Note that the graph crosses the x-axis in two places:
-0.658872343938 and
0.758872343938.
If you would like to work another example, click on Example
If you would like to test yourself by working some problems similar to this
example, click on Problem
If you would like to go back to the equation table of contents, click on
Contents

