EQUATIONS INVOLVING FRACTIONS (RATIONAL EQUATIONS)

Note:

• A rational equation is an equation where at least one denominator contains a variable.

• When a denominator contains a variable, there is a restriction on the domain. The variable cannot take on any number that would cause any denominator to be zero.

• The first step is solving a rational equation is to convert the equation to an equation without denominators. This new equation may be equivalent (same solutions as the original equation) or it may not be equivalent (extraneous solutions).

• The next step is to set the equation equal to zero and solve.

• Remember that you are trying to isolate the variable.

• Depending on the problem, there are several methods available to help you solve the problem.

If you would like an in-depth review of fractions, click on Fractions.

Solve for x in the following equation.

Example 1:

$$\frac{34}{x^{2}-3x+7}+5=2x-3$$

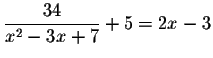
Recall that you cannot divide by zero. Therefore, we must eliminate any values of x that will cause the denominator to have a value of zero. We determine these values by setting

$$\begin{eqnarray*}x^{2}-3x+7 &=&0 \\ && \\ x &=&\displaystyle \frac{3\pm \sqrt{-19}}{2} \end{eqnarray*}$$

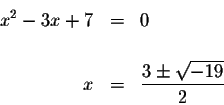
These values of x are not real numbers. What this means is that there is no value of x that will cause the denominator to be zero. This means that there are no restrictions on the values of x.

Simplify the equation by subtracting 5 from both sides of the equation.

$$\begin{eqnarray*}\displaystyle \frac{34}{x^{2}-3x+7}+5 &=&2x-3 \\ && \\ && \\ \displaystyle \frac{34}{x^{2}-3x+7} &=&2x-8 \end{eqnarray*}$$

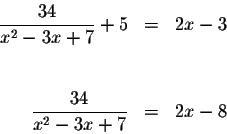
Multiply both sides of the equation by $\left( x^{2}-3x+7\right) .$

$$\begin{eqnarray*}\left( x^{2}-3x+7\right) \left[ \displaystyle \frac{34}{x^{2}-3... ...^{2}-3x+7}\right] &=&\left( x^{2}-3x+7\right) \left[ 2x-8\right] \end{eqnarray*}$$

$$\begin{eqnarray*}34 &=&\left( x^{2}-3x+7\right) \left[ 2x-8\right] \\ && \\ &&... ...8\right) \\ && \\ && \\ 34 &=&2x^{3}-8x^{2}-6x^{2}+24x+14x-56 \end{eqnarray*}$$

$$\begin{eqnarray*}0 &=&2x^{3}-14x^{2}+38x-90 \\ && \\ && \\ 0 &=&x^{3}-7x^{2}+... ...\ && \\ && \\ 0 &=&\left( x-5\right) \left( x^{2}-2x+9\right) \end{eqnarray*}$$

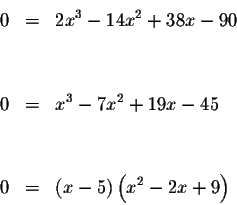
The only way a product can equal zero is if at least one of the factors equals zero.

$$\begin{eqnarray*}If\ x-5 &=&0,\ then\ x=5 \\ && \\ If\ x^{2}-2x+9 &=&0,\ then\ x=\displaystyle \frac{2\pm \sqrt{-32}}{2}. \end{eqnarray*}$$

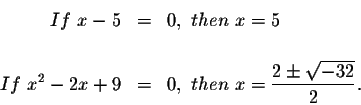
This is not a real number: therefore, $x^{2}-2x+9\neq 0.\$Therefore the only real solution is x=5.

Check the solution x=5 in the original equation for x. If the left side of the equation equals the right side of the equation after the substitution, you have found the correct answer.        

• Left Side: $\qquad \displaystyle \frac{34}{x^{2}-3x+7}+5=\displaystyle \frac{34}{\left( 5\right) ^{2}-3\left( 5\right) +7}+5=7$

  
  

  
  

• Right Side: $\qquad 2x-3=2\left( 5\right) -3=7$.

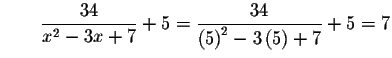
Since the left side of the original equation is equal to the right side of the original equation after we substitute the value 5 for x, then x=5 is a solution.

You can also check your answer by graphing $\quad$

$$\begin{eqnarray*}f(x) &=&\displaystyle \frac{34}{x^{2}-3x+7}+8-2x \end{eqnarray*}$$.

(formed by subtracting the right side of the original equation from the left side). Look to see where the graph crosses the x-axis; that will be the real solution. Note that the graph crosses the x-axis at one place, 5.

This means that there is one real solution and the solution is x=5.

If you would like to work another example, click on Example

If you would like to test yourself by working some problems similar to this example, click on Problem

If you would like to go back to the equation table of contents, click on Contents

[Algebra] [Trigonometry] [Geometry] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA