The Derivatives of Trigonometric Functions

$$\begin{array}{cc}\sin^\prime x=\cos x&\cos^\prime x=-\cos x\\... ...\prime x=\sec x \tan x&\csc^\prime x=-\csc x \cot x \end{array}$$

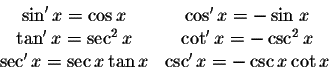
Trigonometric functions are useful in our practical lives in diverse areas such as astronomy, physics, surveying, carpentry etc. How can we find the derivatives of the trigonometric functions?

Our starting point is the following limit:

$$\lim_{x \rightarrow 0} \frac{\sin(x)}{x} = 1\cdot$$

Using the derivative language, this limit means that $\sin'(0) = 1$. This limit may also be used to give a related one which is of equal importance:

$$\lim_{x \rightarrow 0} \frac{\cos(x)-1}{x} = 0$$

To see why, it is enough to rewrite the expression involving the cosine as

$$\frac{\cos(x)-1}{x} = \frac{(\cos(x)-1)(\cos(x) + 1)}{x(\cos(x) + 1)} = \frac{(\cos^2(x)-1)}{x(\cos(x) + 1)}$$

But $\cos^2(x)-1 = -\sin^2(x)$, so we have

$$\lim_{x \rightarrow 0} \frac{\cos(x)-1}{x} = \lim_{x \rightar... ... \rightarrow 0} x \frac{-\sin^2(x)}{x^2(\cos(x) + 1)} = 0 \cdot$$

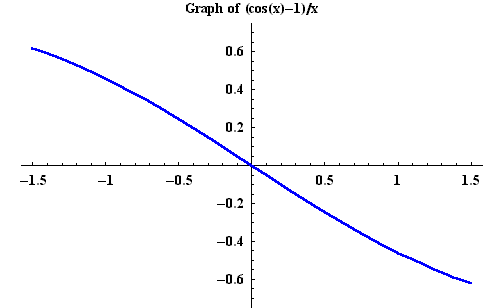
This limit equals $\cos'(0)$ and thus $\cos'(0) = 0$.

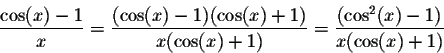
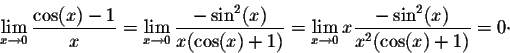
In fact, we may use these limits to find the derivative of $\sin(x)$ and $\cos(x)$ at any point x=a. Indeed, using the addition formula for the sine function, we have

$$\sin(a + h) = \sin(a) \cos(h) + \sin(h) \cos(a) \cdot$$

So

$$\frac{\sin(a + h) - \sin(a)}{h} = \sin(a)\frac{1 - \cos(h)}{h} + \cos(a) \frac{\sin(h)}{h}$$

which implies

$$\lim_{h \rightarrow 0} \frac{\sin(a + h) - \sin(a)}{h} = \cos(a) \cdot$$

So we have proved that $\sin'(a)$ exists and $\sin'(a) = \cos(a)$.

Similarly, we obtain that $\cos'(a)$ exists and that $\cos'(a) = -\sin(a)$.

Since $\tan(x)$, $\cot(x)$, $\sec(x)$, and $\csc(x)$ are all quotients of the functions $\sin(x)$ and $\cos(x)$, we can compute their derivatives with the help of the quotient rule:

$$\begin{array}{llll} \displaystyle \frac{d}{dx} (\tan(x)) = \s... ...style \frac{d}{dx} (\csc(x)) = -\csc(x) \cot(x) \\ \end{array}$$

It is quite interesting to see the close relationship between $\tan(x)$ and $\sec(x)$ (and also between $\cot(x)$ and $\csc(x)$).

From the above results we get

$$\sin''(x) = - \sin(x)\;\;\mbox{and}\;\; \cos''(x) = - \cos(x)\cdot$$

These two results are very useful in solving some differential equations.

Example 1. Let $f(x) = \sin(2 x)$. Using the double angle formula for the sine function, we can rewrite

$$\sin(2 x) = 2 \sin(x) \cos(x)\cdot$$

So using the product rule, we get

$$\frac{d}{dx}\Big(\sin(2x)\Big) = 2 \Big( \cos(x) \cos(x) - \sin(x) \sin(x) \Big) = 2 \Big( \cos^2(x) - \sin^2(x) \Big)$$

which implies, using trigonometric identities,

$$\frac{d}{dx}\Big(\sin(2x)\Big) = 2 \cos(2x)\cdot$$

In fact next we will discuss a formula which gives the above conclusion in an easier way.

Exercise 1. Find the equations of the tangent line and the normal line to the graph of $f(x) = \sec(x) + \tan(x)$ at the point $\left(\displaystyle \frac{\pi}{4}, f\left(\frac{\pi}{4}\right)\right)$.

Answer.

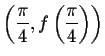Exercise 2. Find the x-coordinates of all points on the graph of $f(x) = x +2\cos(x)$ in the interval $[0,\pi]$ at which the tangent line is horizontal.

Answer.

[Back] [Next] [Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA