 The Geometric Series
The Geometric Series The Geometric Series
The Geometric Series ![]()
The series inside the parentheses is the familiar geometric series with
![]() . Thus, this series sums to
. Thus, this series sums to
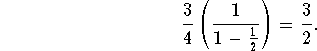
The summation trick on the previous page does not work for all values of q. Consider for instance q=1. Clearly, the sum
![]()
does not add up to a finite number! One says that this series diverges (= is not convergent). This does not have much to do with the fact that in the end we "divide by 0"; try q=2 or q=-1.
The problem lies much deeper. The sad truth is that many of the algebraic properties of finite sums do not work for infinite sums--troubling mathematicians over the centuries! So let's be very cautious and try again. This time we only consider finite sums and then take the limit! Let
![]()
multiply both sides by q
![]()
then subtract the second line from the first:
![]()
For ![]() , we can solve this for
, we can solve this for ![]() :
:
![]()
It is not hard to see what happens when we consider
![]()
The identity
![]()
is valid exactly when -1<q<1.
Find the sum of the series
![]()
Click here for the answer or to continue.