Absolute Convergence of Improper Integrals

Since most of the tests of convergence for improper integrals are only valid for positive functions, it is legitimate to wonder what happens to improper integrals involving non positive functions. First notice that there is a very natural way of generating a positive number from a given number: just take the absolute value of the number. So consider a function f(x) (not necessarily positive) defined on [a,b]. Then let us consider the positive function |f(x)| still defined on [a,b]. It is easy to see that both functions f(x) and |f(x)| will exhibit the same kind of improper behavior. Therefore, one may ask naturally what conclusion do we have if we know something about the integral

We have the following partial answer:

If the integral is convergent, then the integral is also convergent.

We have to be careful the converse is not true. Indeed, the improper integral

is convergent while the improper integral

is divergent. This is quite hard to show. On the other hand, it shows that the convergence of 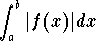carries more information than just convergence. In this case, we say that the improper integral 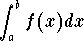is absolutely convergent. And if the improper integral 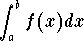is convergent while the improper integral 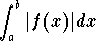is divergent, we say it is conditionally convergent.

Example. Establish the convergence or divergence of

Answer. We have an improper integral of Type II. Since the function is not positive on , we will investigate whether the given improper integral is absolutely convergent. Hence we must consider the improper integral

Let us check whether we have a Type I behavior. Clearly the point 0 is a bad point. We leave it as an exercise to check that the function 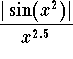is indeed unbounded around 0. So we must split the integral and write

First let us take care of the integral

We know that when . Hence we have

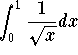when . Since the integral is convergent via the p-test, the limit test enables us to conclude that the integral

is convergent. Next we take care of the improper integral

We can not use the limit test since the function does not have a nice behavior around . But we know that for any number x. Hence we have

for any . Since the improper integral 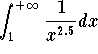is convergent via the p-test, the basic comparison test implies that the improper integral

is convergent. Therefore putting the two integrals together, we conclude that the improper integral

is convergent. This clearly implies that the improper integral

is absolutely convergent.

Example. Show that the improper integral

is convergent.
Answer. As we mentioned before, this improper integral is not absolutely convergent. So there is no need of considering the absolute value of the function. Note that the integral is improper obviously because of . 0 is not a bad point since

But even if it is not a bad point, we will isolate it by writing

The integral is not improper. So we concentrate on the integral

We know by definition that

Now consider the proper integral 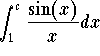. An integration by parts gives

Since

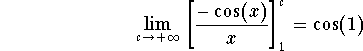
and

we get

Note now that the improper integral 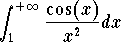is in fact absolutely convergent. Indeed, we have

and since by the p-test the improper integral 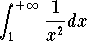is convergent, the basic comparison test implies the desired conclusion, that is 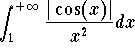is convergent. Therefore the improper integral 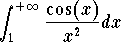is convergent. Since

then the improper integral 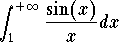is convergent.

[Geometry] [Algebra] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra] [Trigonometry]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA