Integrating Powers and Product of Sines and Cosines: Example 2

Evaluate

Solution. First let us find the antiderivative . We have

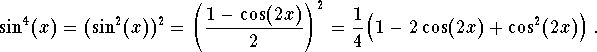
We should continue with as well and get

Therefore, we have

which implies

[Calculus] [More Examples] [Challenging Problems] [Geometry] [Algebra] [Trigonometry ] [Differential Equations] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA