Rational Expressions of Trigonometric Functions
Rational Expressions of Trigonometric Functions
Expressions like
are called rational expressions of sin and cos. Note that all the other trigonometric functions are rational functions of sin and cos. The main idea behind integrating such functions is the general substitution
In order to have better feeling how things do work, remember the trigonometric formulas
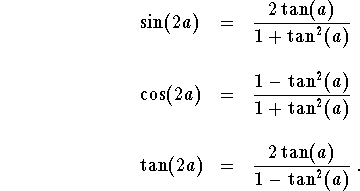
It is not hard to generate similar formulas for 
, 
, and
from the above formulas. Therefore, any rational function
will be transformed into a rational function of
t via the above formulas. For example, we have
where 
. Note that in order to complete the
substitution we need to find dx as function of t and dt. Since
, we get
Now we are ready to integrate rational functions of sin and cos or at
least transform them into integrating rational functions.
Check the following examples to see how this technique works:
S.O.S MATHematics home page 