Calculus- Techniques of Integration: Substitution-Example1
Calculus- Techniques of Integration: Substitution-Example1
Find
Solution. It is clear that once we develop
the 
through the binomial formula, we will get a
polynomial function easy to integrate. But it is clear that this will
take a lot of time with big possibility of doing mistakes !!
Let us consider the substitution 
(the reason behind is
the presence of x in the integral since the derivative of 
is 2x). Indeed, we have du = 2x dx and therefore
We may check that the new integral is easier to handle since
.
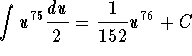Hence
which does not complete the answer since the indefinite integral
is a function of x not of
u. Therefore, we have to go back and replace u by u(x):
S.O.S MATHematics home page 