The Ratio Test

The general term of the series is 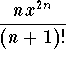tex2html_wrap_inline52 , thus the absolute ratios have the form:

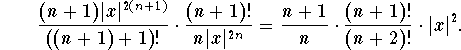
displaymath46

Now since ,

we can continue computing the limit of the absolute ratios as

no matter which value we consider for x. Since 0<1, the ratio test lets us conclude that this series converges for all real x. The radius of convergence of this series is .