 Stirling's Formula
Stirling's Formula

An important formula in applied mathematics as well as in probability is the Stirling's formula known as
where  is used to indicate that the ratio of the two sides goes to 1 as n goes to
is used to indicate that the ratio of the two sides goes to 1 as n goes to  .
In other words, we have
.
In other words, we have
or
Proof of the Stirling's Formula
First take the log of n! to get
Since the log function is increasing on the interval
 ,
we get
,
we get
for  .
Add the above inequalities, with
.
Add the above inequalities, with
 ,
we get
,
we get
Though the first integral is improper, it is easy to show that in fact it is convergent. Using the antiderivative of  (being
(being
 ), we get
), we get
Next, set
We have
Easy algebraic manipulation gives
Using the Taylor expansion
for
-1 < t < 1, we get
This implies
We recognize a geometric series. Therefore we have
From this we get
- 1.
- the sequence
 is decreasing;
is decreasing;
- 2.
- the sequence
 is increasing.
is increasing.
This will imply that  converges to a number C with
converges to a number C with
and that
C > d1 - 1/12 = 1 - 1/12 = 11/12. Taking the exponential of dn, we get
The final step in the proof if to show that
 .
This will be done via Wallis formula (and Wallis integrals). Indeed, recall the limit
.
This will be done via Wallis formula (and Wallis integrals). Indeed, recall the limit
Rewriting this formula, we get
Playing with the numbers, we get
Using the above formula
we get
Easy algebra gives
since we are dealing with constants, we get in fact
 .
This completes the proof of the Stirling's formula.
.
This completes the proof of the Stirling's formula.

[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Tue Dec 3 17:39:00 MST 1996
Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Stirling's Formula
Stirling's Formula Stirling's Formula
Stirling's Formula






 is increasing.
is increasing.

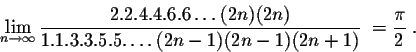




 S.O.S MATHematics home page
S.O.S MATHematics home page 