 Convergence of Series
Convergence of Series Convergence of Series
Convergence of Series

Consider the series ![]() and its associated
sequence of partial sums
and its associated
sequence of partial sums ![]() . We will say that
. We will say that ![]() is convergent if and only if the sequence
is convergent if and only if the sequence
![]() is convergent. The total sum of the series is the limit of
the sequence
is convergent. The total sum of the series is the limit of
the sequence ![]() , which we will denote by
, which we will denote by
![]()
So as you see the convergence of a series is related to the
convergence of a sequence. Many do some serious mistakes in confusing
the convergence of the sequence of partial sums ![]() with the
convergence of the sequence of numbers
with the
convergence of the sequence of numbers ![]() .
.
Basic Properties.
![]()
for any ![]() .
.
This implies in particular that if we know sequence of partial sums
![]() , one may generate the numbers
, one may generate the numbers ![]() since we have
since we have
![]()
![]()
In particular, if the sequence we are trying to add does not converge to 0, then the associated series is divergent.
![]()
converges if and only if |q|<1. Moreover we have
![]()
![]()
is convergent and moreover we have
![]()
Example. Show that the series
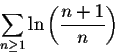
is divergent, even though
![]()
Answer. Note that for any ![]() , we have
, we have
![]()
Hence we have (for the associated partial sums)
![]()
Since ![]() ,
then we have
,
then we have
![]()
which implies that the series is divergent. Indeed, we do have
![]()
since
![]()
which implies
![]()
Example. Check that the following series is convergent and find its total sum
![]()
Answer. We have
![]()
Using the above properties, we see here that we are dealing with two geometric series which are convergent. Hence the original series is convergent and we have
![]()
which gives
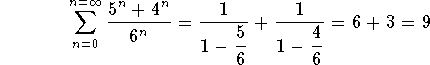
Example. Check that the following series is convergent and find its total sum

Answer. First we need to clean the expression (by using algebraic manipulations)
![]()
We recognize a geometric series. Since 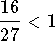 , then the series is convergent and we have
, then the series is convergent and we have
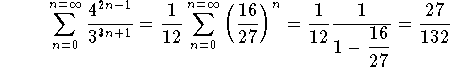

 S.O.S MATHematics home page
S.O.S MATHematics home page 
Tue Dec 3 17:39:00 MST 1996