More Examples on Series

Problem 1: Test for convergence

.

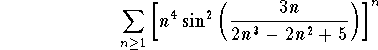Answer: Since we have a power n in the series, we will use the Root-Test. Set

.

We have

.

Since

,

and

,

we get

.

But,

.

Hence,

.

Therefore, by the Root-Test, the series

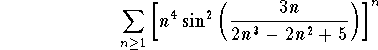
is divergent.

Problem 2: Test for convergence

.

Answer: The sum of two series converges, if both of the sums converge. Hence the series

$$\sum$$$${\frac{(3n)!+4^{n+1}}{(3n+1)!}}$$

will diverge, if we can show that

$$\sum$$$${\frac{(3n)!}{(3n+1)!}}$$

diverges, while the series

$$\sum$$$${\frac{4^{n+1}}{(3n+1)!}}$$

converges. Since

$${\frac{(3n)!}{(3n+1)!}}$$ = $${\frac{1}{3n+1}}$$,

and

$${\frac{1}{3n+1}}$$ $$\approx$$ $${\frac{1}{3n}}$$

and the series

$$\sum$$$${\frac{1}{3n}}$$

diverges by the p-test, we conclude that

$$\sum$$$${\frac{(3n)!}{(3n+1)!}}$$

diverges.

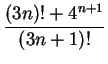
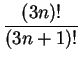
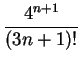
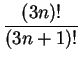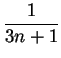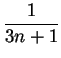
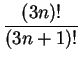
On the other hand,

$$\sum$$$${\frac{4^{n+1}}{(3n+1)!}}$$

converges by the ratio test:

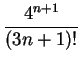
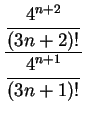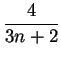$$\lim_{n\to\infty}^{}$$$${\frac{\displaystyle\frac{4^{n+2}}{(3n+2)!}}{\displaystyle\frac{4^{n+1}}{(3n+1)!} }}$$ = $$\lim_{n\to\infty}^{}$$$${\frac{4}{3n+2}}$$ = 0 < 1.

This establishes that

$$\sum$$$${\frac{(3n)!+4^{n+1}}{(3n+1)!}}$$

diverges.

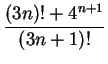
Problem 3: Test for convergence

.

Answer: We will use the Ratio-Test (try to use the Root-Test to see how difficult it is). Set

.

We have

.

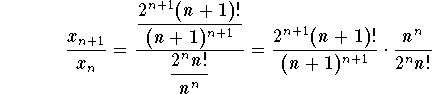Algebraic manipulations give

,

since

.

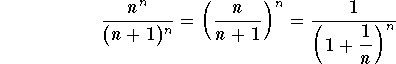Hence, we have

,

which implies

.

Since , we conclude, from the Ratio-Test, that the series

is convergent.

Problem 4: Determine whether the series

is convergent or divergent.

Answer: Consider the function

.

It is easy to check that f(x) is decreasing on . Hence, for any , we have for any ,

,

which implies

,

that is,

.

Using this inequality, we get

,

since

.

Since

,

we deduce that the partial sums associated to the series

are not bounded. Therefore, the series

is divergent.

Remark: Note that the proof given above is the proof of the Integral-Test. In other words, we may have just used to Integral-Test to get the conclusion. Also, the series given here is part of a type of series called Bertrand series defined as

.

[Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA