Basic Definitions
Basic Definitions
It is an amazing fact that by adjoining the imaginary unit i to the real numbers we obtain a complete number field called `` The Complex Numbers." In this amazing number field every algebraic equation in z with complex coefficients
has a solution. To prove this fact we need Liouville's Theorem, but to get started using complex numbers all we need are the following basic rules.
for some real a and b.
Notice that rules 4 and 5 state that we can't get out of the complex numbers by adding (or subtracting) or multiplying two complex numbers together. What about dividing one complex number by another? Is the result another complex number? Let's ask the question in another way. If you are given four real numbers a,b,c and d, can you find two other real numbers x and y so that
As an exercise in using rules 1 through 5, multiply both sides of the above equation by c + di and then solve for x and y to prove that the answer to our question is yes.( Click on help for a solution.)
OK, so we can divide by c + di if c and d are not both zero. But there is a much easier way to do division.
Notice that
We say that c+di and c-di are complex conjugates. To simplify a complex fraction, multiply the numerator and the denominator by the complex conjugate of the denominator.
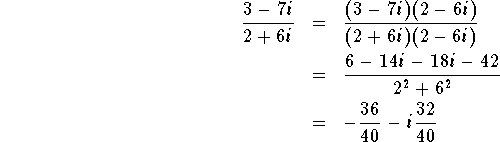
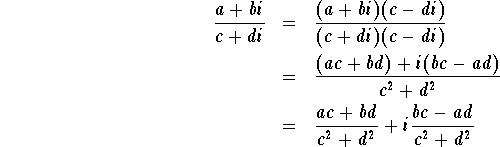
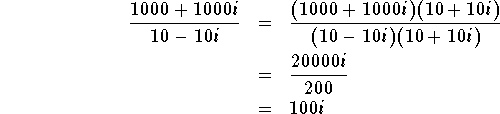
If z= a+bi is a complex number and a and b are real, we say that a is the real part of z and that b is the imaginary part of z and we write
Exercise:
Find 
and 
.
(Solution)
If z=a +bi is a complex number with real part a and imaginary part
b, then we denote the complex conjugate of z by 
.
Exercise:
Write 
in standard form.
Exercise:
Prove that 
for any pair
of complex numbers and similarly 
.
Exercise:
Prove that 
for any
integer n.
The magnitude or modulus of a complex number z is denoted |z| and defined as
Notice that 
. (proof.)
Exercise:
Prove that 
.
(Solution)
S.O.S MATHematics home page 