Differential Equations Practice Exams

Answers

Problem 1: Use variation of parameters to find the general solution to

First we need to solve the homogeneous equation y''' - y' = 0. Its characteristic equation is . It is easy to see that its root are r=0,1,-1. Therefore we have .
Second we need to find a particular solution using the variation of parameters technique. We have , where u', v', and w' are solution to the system

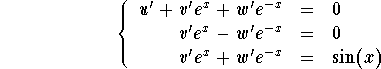
Easy calculations give

Integration by parts, will give (you are encouraged to do it)

Hence we have

which implies that once u, v, w are plugged into the formula giving . Therefore the general solution is given by:

Problem 2. Find the solution to the initial value problem

where

Since g(t) is a step function, we need to use Laplace Transform to solve this problem. Once we attack the equation by , we get

which implies . Using the initial condition, we get

After easy calculations, we obtain

Since , we deduce

Hence

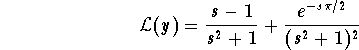
In order to find y, we need to use the inverse Laplace transform. First we have

which implies

The hard part concerns the second term . First let us find the inverse Laplace without the exponential. First we know that

Using the derivative formula, we get

Therefore, we have

Using the formula , we get

Therefore, we have

Problem 3. Find the Laplace transform of

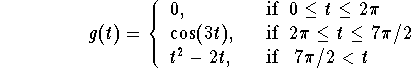
We have

Hence . Using the formula , we get

But which implies

[Next Exam] [Calculus] [CyberExam]

S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA