- a)
-
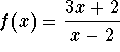 .
.
- b)
-
 .
.
- c)
-
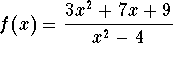 .
.
- d)
-
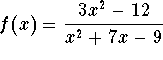 .
.
- e)
- None of the above.
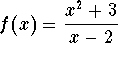 .
.
- a)
- f(x)=x+5.
- b)
- f(x)=2x-1.
- c)
-
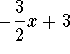 .
.
- d)
- x+2.
- e)
- None of the above.
- a)
-
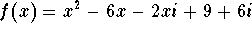 .
.
- b)
-
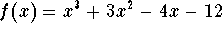 .
.
- c)
-
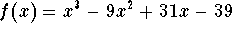 .
.
- d)
-
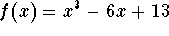 .
.
- a)
- 1.
- b)
- -1.
- c)
- 3.
- d)
-
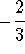 .
.
- e)
- None of the above.
- a)
- 3x-2.
- b)
- 3x+2.
- c)
- 7x+1.
- d)
- 7x-3.
- e)
- None of the above.
- a)
- 20-24i.
- b)
- 12-11i.
- c)
- -4-46i.
- d)
- 48-46i.
- e)
- None of the above.
![]()
where y is the height in feet and x is the horizontal distance in feet. Find the maximum height of the ball.
- a)
- 905 feet.
- b)
- 50 feet.
- c)
- 30 feet.
- d)
- 800 feet.
- e)
- None of the above.
- a)
-
 .
.
- b)
-
 .
.
- c)
-
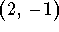 .
.
- d)
-
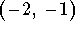 .
.
- e)
- None of the above.
- a)
- 13.
- b)
- 1.
- c)
- -14.
- d)
- 8.
- e)
- None of the above.
![]()
- a)
- The graph of g(x) is the graph of f(x) shifted to the right 4 units, and up 3 units.
- b)
- The graph of g(x) is the graph of f(x) stretched downward 4 units, and 3 units to the right.
- c)
- The graph of g(x) is the graph of f(x) shifted to the left 4 units, and up 3 units.
- d)
- There is not enough information to answer this question.
- e)
- None of the above.
- a)
- -13.
- b)
- 3.
- c)
- 35.
- d)
- -19.
- e)
- None of the above.
- a)
- 15.
- b)
- 1.
- c)
- 3.
- d)
- 5.
- e)
- None of the above.
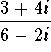 . Find the value of a.
. Find the value of a.
- a)
-
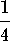 .
.
- b)
-
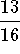 .
.
- c)
-
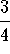 .
.
- d)
-
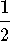 .
.
- e)
- None of the above.
- a)
- 1.
- b)
- 2.
- c)
- 3.
- d)
- 4.
- e)
- None of these.
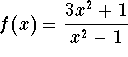 .
.
- a)
-
 .
.
- b)
- (-1,1).
- c)
- All real numbers except
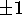 .
.
- d)
-
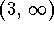 .
.
- e)
- None of the above.
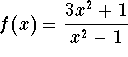 .
.
- a)
-
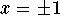 .
.
- b)
- y=3.
- c)
-
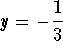 .
.
- d)
- y=-1.
- e)
- None of the above.
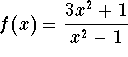 .
.
- a)
- y=3.
- b)
-
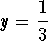 .
.
- c)
- x=1.
- d)
-
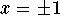 .
.
- e)
- None of the above.
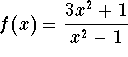 at x=10,000,000,000.
at x=10,000,000,000.
- a)
- 30,000,000,000
- b)
- 29,999,999,999
- c)
- 9
- d)
- 3
- e)
- None of the above.
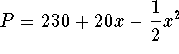 . How much advertising will yield a
maximum profit?
. How much advertising will yield a
maximum profit?
- a)
- $43,000.
- b)
- $ 2,000.
- c)
- $63,000.
- d)
- $ 1,000.
- e)
- None of the above.
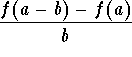 .
.
- a)
-
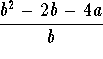 .
.
- b)
-
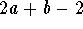 .
.
- c)
-
 .
.
- d)
- 1.
- e)
- None of the above.
- a)
- No.
- b)
- Yes.
- c)
- Depends on the radius.
- d)
- Yes, if the center is at the origin.
- e)
- None of the above.
- a)
- No.
- b)
- Yes.
- c)
- Depends on the axis of symetry.
- d)
- Yes, if the vertex is at the origin.
- e)
- None of the above.
 represents the volume
of a cone. Find x in terms of the other variables.
represents the volume
of a cone. Find x in terms of the other variables.
- a)
-
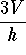 .
.
- b)
-
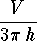 .
.
- c)
-
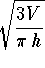 .
.
- d)
-
 .
.
- e)
- None of the above.
- a)
- 3x-9.
- b)
- 3x+9.
- c)
-
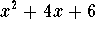 .
.
- d)
-
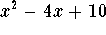 .
.
- e)
- None of the above.
- a)
-
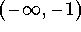 .
.
- b)
-
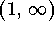 .
.
- c)
-
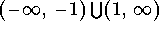 .
.
- d)
-
 .
.
- e)
- None of the above.