Existence and Uniqueness of Solutions: Example 1

Example: Suppose the differential equation 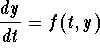tex2html_wrap_inline14 satisfies the Existence and Uniqueness Theorem for all values of y and t. Suppose tex2html_wrap_inline20 and tex2html_wrap_inline22 are two solutions to this differential equation.

1.
What can you say about the behavior of the solution of the solution y(t) satisfying the initial condition y(0)=1?
Hint: Draw the two solutions tex2html_wrap_inline28 and tex2html_wrap_inline30 .
2.
Address the behavior of y(t) as t approaches tex2html_wrap_inline36 , and as t approaches tex2html_wrap_inline40 .

Answer:

1.
First let us draw the graphs of tex2html_wrap_inline11 and tex2html_wrap_inline13 .


Since we have tex2html_wrap_inline15 , we deduce from the Existence and Uniqueness Theorem that for all t, we have

displaymath19

In particular, y(t) has the line y=t as an oblique asymptote which answers the second question.

We cannot predict that y(t) is an increasing function.

[Differential Equations] [Slope Field]
[Geometry] [Algebra] [Trigonometry ]
[Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page


Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA