Integrating Factor Technique: Example

Find all the solutions to

Solution: Note that this equation is in fact homogeneous. But let us use the technique of exact and nonexact to solve it. Let us follow these steps:

(1)

We rewrite the equation to get

Hence, and .

(2)

We have

,

which clearly implies that the equation is not exact.

(3)

Let us find an integrating factor. We have

.

Therefore, an integrating factor u(x) exists and is given by

(4)

The new equation is

,

which is exact. (Check it!)

(5)

Let us find F(x,y). Consider the system:

(6)

Let us integrate the first equation. We get

(7)

Differentiate with respect to y and use the second equation of the system to get

,

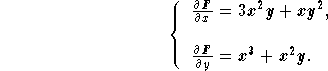
which implies , that is, is constant. Therefore, the function F(x,y) is given by

We don't have to keep the constant C due to the nature of the solutions (see next step).

(8)

All the solutions are given by the implicit equation

Remark: Note that if you consider the function

,

then we get another integrating factor for the same equation. That is, the new equation

is exact. So, from this example, we see that we may not have uniqueness of the integrating factor. Also, you may learn that if the integrating factor is given to you, the only thing you have to do is multiply your equation and check that the new one is exact.

[Differential Equations] [First Order D.E.] [Integrating Factor Technique] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA