Higher Order Linear Equations: Introduction and Basic Results
Higher Order Linear Equations: Introduction and Basic Results
Let us consider the equation
,
and its associated homogeneous equation
The following basic results hold:
be solutions of the equation (H).
Then, the function
is also solution of the equation (H). This solution is called
a linear combination of the functions 
;
where 
are arbitrary constants and
are n solutions of the equation (H)
such that,
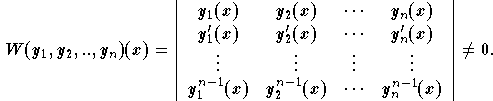
In this case, we will say that are linearly
independent. The function 
is called the
Wronskian of 
. We have
Therefore, 
, for some 
, if and only if, 
for every x;
where are arbitrary constants,
are linearly independents solutions of the
associated homogeneous equation (H), and 
is a particular
solution of (NH).
S.O.S MATHematics home page 