 Homogeneous Linear Equations With Constant Coefficients
Homogeneous Linear Equations With Constant Coefficients

Consider the nth-order linear equation with constant coefficients
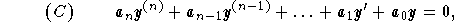
with 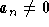 . In order to generate n linearly independent
solutions, we need to perform the following:
. In order to generate n linearly independent
solutions, we need to perform the following:
-
- (1)
- Write the characteristic equation

Then, look for the roots. These roots will be of two natures:
simple or multiple. Let us show how they generate independent
solutions of the equation(H).
- (2)
- First case: Simple root
Let r be a simple root of the characteristic equation.
- (2.1)
- If r is a real number, then it generates the solution
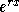 ;
;
- (2.2)
- If
 is a complex root, then since the
coefficients of the characteristic equation are real,
is a complex root, then since the
coefficients of the characteristic equation are real,  is also a root. The two roots generate the two solutions
is also a root. The two roots generate the two solutions
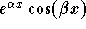 and
and  ;
;
- (3)
- Second case: Multiple root
Let r be a root of the characteristic equation with multiplicity
m. If r is a real number, then generate the m independent
solutions
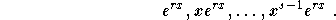
If  is a complex number, then
is a complex number, then  is also a root with multiplicity m. The two complex roots
will generate 2m independent solutions
is also a root with multiplicity m. The two complex roots
will generate 2m independent solutions
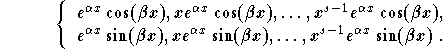
Using properties of roots of polynomial equations, we will generate
n independent solutions 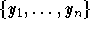 . Hence, the general
solution of the equation (H) is given by
. Hence, the general
solution of the equation (H) is given by
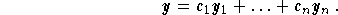
Therefore, the real problem in solving (H) has to do more with
finding roots of polynomial equations. We urge students to
practice on this.
Example: Find the general solution of

Solution: Let us follow these steps:
-
- (1)
- Characteristic equation

Its roots are the
complex numbers
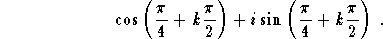
In the
analytical form, these roots are
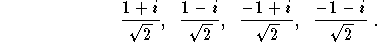 ;
;
- (2)
- Independent set of solutions
- (2.1)
- The complex roots
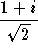 and
and
 generate the two solutions
generate the two solutions
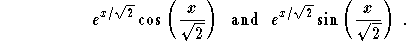 ;
;
- (2.2)
- The complex roots
 and
and
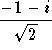 generate the two solutions
generate the two solutions
 ;
;
- (3)
- The general solution is
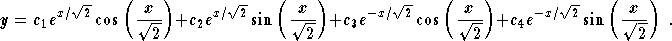
As you may have noticed in this example, complex numbers do get involved
very much in this kind of problem...

[Differential Equations]
[First Order D.E.]
[Second Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Homogeneous Linear Equations With Constant Coefficients
Homogeneous Linear Equations With Constant Coefficients  Homogeneous Linear Equations With Constant Coefficients
Homogeneous Linear Equations With Constant Coefficients 
![]()
![]() . In order to generate n linearly independent
solutions, we need to perform the following:
. In order to generate n linearly independent
solutions, we need to perform the following:
![]()
![]()
![]() is a complex number, then
is a complex number, then ![]() is also a root with multiplicity m. The two complex roots
will generate 2m independent solutions
is also a root with multiplicity m. The two complex roots
will generate 2m independent solutions
![]()
![]()
![]()
![]()
![]()
![]() ;
; ![]() ;
;  and
and
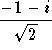 generate the two solutions
generate the two solutions
![]() ;
; ![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page 