 LAPLACE TRANSFORM
LAPLACE TRANSFORM LAPLACE TRANSFORM
LAPLACE TRANSFORM

Let f(t) be a function defined on
The domain of
then f(t)=g(t) for
This is a very important formula because of its use in differential
equations.
where
is called the Heaviside function at c. It plays a major role when
discontinuous functions are involved. We have
When c=0, we write
and
Hence,
Example: Find
Solution: Since
we get
Hence,
In particular, we have
The next example deals with the Gamma Function.
![]() . The Laplace
transform of f(t) is a new function defined as
. The Laplace
transform of f(t) is a new function defined as
![]()
![]() is the set of
is the set of ![]() , such
that the improper integral converges.
, such
that the improper integral converges.
![]() and M such that
and M such that
![]()
Let f(t) be a function piecewise continuous on [0,A] (for every
A>0) and have an exponential order at infinity with ![]() . Then, the Laplace transform
. Then, the Laplace transform ![]() is defined for
is defined for ![]() , that is
, that is ![]() .
.
Let f(t), and g(t), be two functions
piecewise continuous with an exponential order at infinity. Assume that
![]()
![]() , for every B > 0, except maybe
for a finite set of points.
, for every B > 0, except maybe
for a finite set of points.
![]() , then
, then
![]()
![]() ,
for
,
for ![]() , are piecewise continuous and have an exponential
order at infinity. Then we have
, are piecewise continuous and have an exponential
order at infinity. Then we have
![]()
![]()
![]() is the derivative of order n of the function F.
is the derivative of order n of the function F.
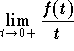 , is
finite. Then we have
, is
finite. Then we have
![]()
The function
![]()
![]()
![]() . The notation
. The notation
![]() , is also used to denote the Heaviside function.
, is also used to denote the Heaviside function.
![]() ,
, ![]()
![]()
![]() .
. ![]() ,
, ![]()
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page 
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA