 Method of Undetermined Coefficients: Example
Method of Undetermined Coefficients: Example

Find a particular solution to the
equation
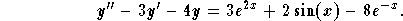
Solution: Let us follow these steps:
-
- (1)
- First, we notice that the conditions are satisfied to invoke
the method of undetermined coefficients.
- (2)
- We split the equation into the following three equations:
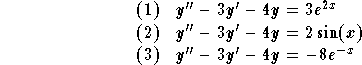
- (3)
- The root of the characteristic equation
 are
r=-1 and r=4.
are
r=-1 and r=4.
- (4.1)
- Particular solution to Equation (1):
-
- Since
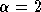 , and
, and 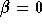 , then
, then 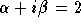 ,
which is not one of the roots. Then s=0.
,
which is not one of the roots. Then s=0.
-
- The particular solution is given as

-
- If we plug it into the equation (1), we get
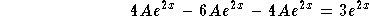 ,
,
which implies A = -1/2, that is,

- (4.2)
- Particular solution to Equation (2):
-
- Since
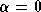 , and
, and 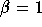 , then
, then 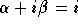 ,
which is not one of the roots. Then s=0.
,
which is not one of the roots. Then s=0.
-
- The particular solution is given as
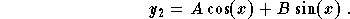
-
- If we plug it into the equation (2), we get
 ,
,
which implies

Easy calculations give
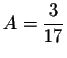 ,
and
,
and
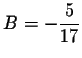 ,
that is
,
that is
- (4.3)
- Particular solution to Equation (3):
-
- Since
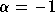 , and
, and 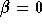 , then
, then 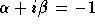 which is one of the roots. Then s=1.
which is one of the roots. Then s=1.
-
- The particular solution is given as

-
- If we plug it into the equation (3), we get
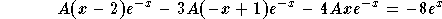 ,
,
which implies
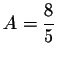 ,
that is
,
that is
- (5)
- A particular solution to the original equation is

[Differential Equations]
[First Order D.E.]
[Second Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Method of Undetermined Coefficients: Example
Method of Undetermined Coefficients: Example  Method of Undetermined Coefficients: Example
Method of Undetermined Coefficients: Example 
![]()
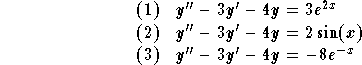
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
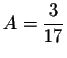 ,
and
,
and
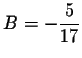 ,
that is
,
that is
![]()
![]() ,
, 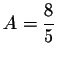 ,
that is
,
that is

 S.O.S MATHematics home page
S.O.S MATHematics home page 