

Find the Hermite Polynomials of order 1 and 3.
Recall that the recurrence relations are given by
We have to evaluate these coefficients for k=1 and k=3, with initial conditions a0=0, a1=1.
When k=1,
Consequently all odd coefficients other than a1 will be zero. Since a0=0, all even coefficients will be zero, too. Thus
H1(t)=t.
When k=3,
and
Consequently all odd coefficients other than a1 and a3 will be zero. Since a0=0, all even coefficients will be zero, too. Thus

[Back]
[Exercises]
[Next]
[Algebra]
[Trigonometry]
[Complex Variables]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page

1998-07-08
Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA



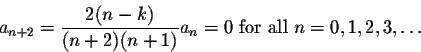

 S.O.S MATHematics home page
S.O.S MATHematics home page 