Complex Eigenvalues
Complex Eigenvalues
Consider the linear homogeneous system
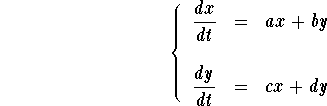
The Characteristic polynomial is
In this section, we consider the case when the above quadratic
equation has complex roots (that is if 
). The
roots (eigenvalues) are
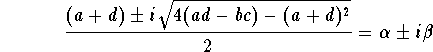
where
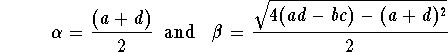
In this case, the difficulty lies with the definition of
In order to get around this difficulty we use Euler's formula
Therefore, we have
In this case, the eigenvector associated to 
will have complex components.
Example. Find the eigenvalues and eigenvectors of the matrix
Answer. The characteristic polynomial is
Its roots are
Set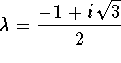 
. The
associated eigenvector V is given by the equation 
. Set
The equation translates into
Since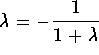 
, then the two
equations are the same (which should have been expected, do you see
why?). Hence we have 
which implies that an
eigenvector is
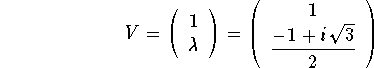
We leave it to the reader to show that for the eigenvalue
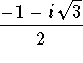, the eigenvector is
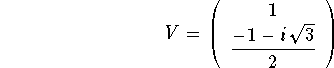
Let us go back to the system
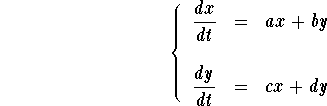
with complex eigenvalues 
. Note that if V, where
is an eigenvector associated to 
, then the vector
(where 
is the conjugate of v) is an eigenvector associated
to 
. On the other hand, we have seen that
are solutions. Note that these solutions are complex functions. In order to find real solutions, we used the above remarks. Set
then we have
which gives
Similarly we have
Putting everything together we get
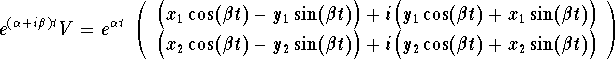
Clearly this implies 
where
It is easy to see that we have
Since the sum and difference of solutions lead to another solution,
then both 
and 
are solutions of the system. These are real
solutions. It is very easy to check in fact that they are linearly
independent. Let us summarize the above technique.
Summary (of the complex case). Consider the system
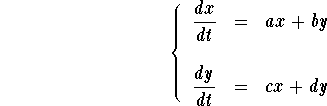
and find its roots
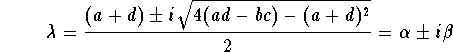
we are assuming that . Note that at this
step, you need to know 
and 
. The common mistake is to
forget to divide by 2.
. Write down the eigenvector as
where 
and 
are arbitrary numbers. Note that in this case,
we have
Example. Consider the harmonic oscillator
Find the general solution using the system technique.
Answer. First we rewrite the second order equation into the system
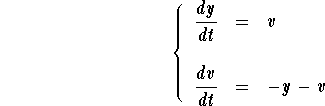
The matrix coefficient of this system is
We have already found the eigenvalues and eigenvectors of this matrix. Indeed the eigenvalues are
Hence we have
The eigenvector associated to is
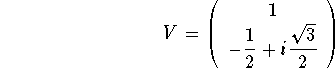
Next we write down the two linearly independent solutions
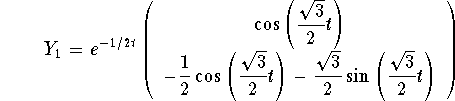
and
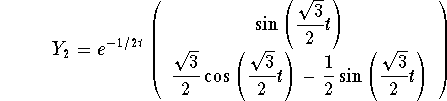
The general solution of the equivalent system is
or
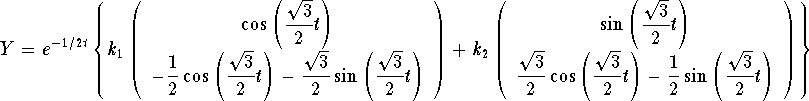
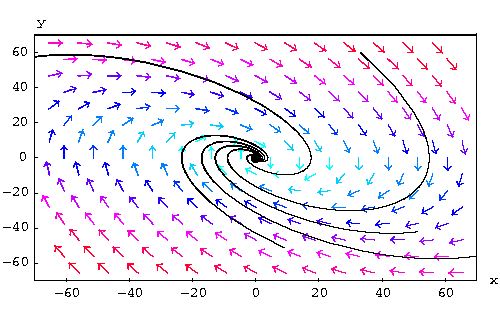
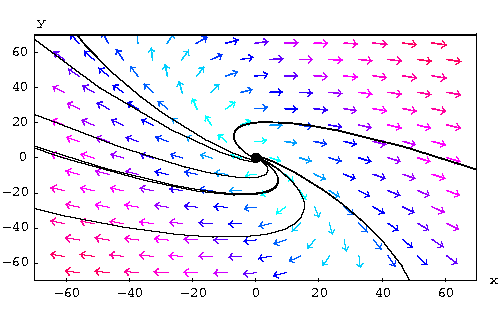
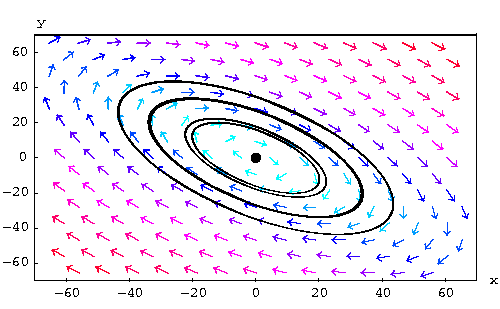
Below we draw some solutions. Notice how the solutions spiral and dye
at the origin (see the discussion below)
|
Since we are looking for the general solution of the differential equation, we only consider the first component. Therefore we have
You may want to check that the second component is just the derivative
of y.
Below we draw some solutions for the differential equation
|
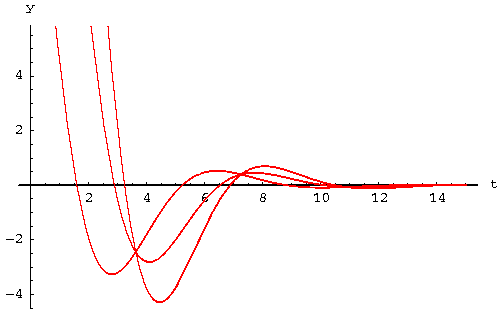
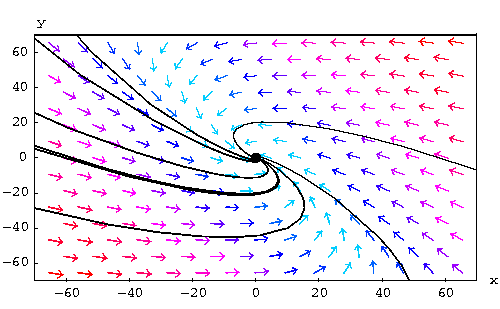
Qualitative Analysis of Systems with Complex Eigenvalues.
Recall that in this case, the general solution is given by
The behavior of the solutions in the phase plane depends on the real
part . Indeed, we have three cases:
. The
solutions tend to the origin (when 
) while
spiraling. In this case, the equilibrium point is called a
spiral sink.
|
The
solutions explode or get away from the origin (when ) while spiraling. In this case, the equilibrium point is
called a spiral source.
|
The
solutions are periodic. This means that the trajectories are closed
curves or cycles. In this case, the equilibrium point is
called a center.
|
S.O.S MATHematics home page 