Answer to Example2

Example: Consider a harmonic oscillator for which the differential equation is

,

and suppose that mass m=1, the damping constant , and the spring constant . Rewrite this equation as a linear system of differential equations. Solve it, then find the particular solution which satisfies the initial conditions

Answer. Set v=y'. Then we have

This gives us the system

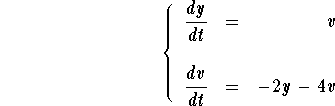
which in matrix form may be rewritten as

where

In order to solve this system, we need the characteristic equation

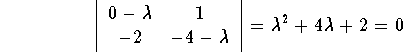
Its roots are given by the quadratic formulas

Note that you have to be very careful here since any mistake at finding correctly the roots will generate a far bigger mistakes and waist of time!!
Next we need to find the associated eigenvectors.

Case . Denote by the associated eigenvector. The system giving is

Since

(which you should check as an exercise), then the two equations are identical. Hence we take . If we choose , we get

Case . Similar calculations give the associated eigenvector

Therefore the general solution is given by

where and are two parameters.

From the above equation giving Y, we may find the solution y to our second differential equation as

We are almost done except that we need to find the specific solution which satisfies the initial condition

These two conditions imply

The second equation gives

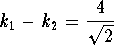since , we get which implies . Hence we have

which implies

and

which yields

Next Example:

[Differential Equations] [First Order D.E.] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA