 Qualitative Analysis of Linear Systems
Qualitative Analysis of Linear Systems

In this page, we will summarize the behavior of the solutions of
linear systems. First consider the linear system
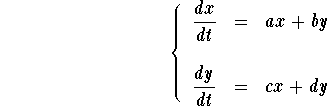
The associated eigenvalues are the roots of the characteristic polynomial
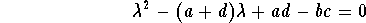
Depending on the eigenvalues, the solutions have different behavior.
-

- Two Real nonzero eigenvalues. We have three
cases:
-

- The two eigenvalues
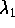 and
and 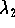 are
positive (with
are
positive (with 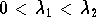 ). When
). When 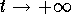 , the solutions explode tangent to the straight-line solution
associated to the eigenvalue
, the solutions explode tangent to the straight-line solution
associated to the eigenvalue 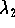 .
.
In this case the equilibrium point is a source.
-

- The two eigenvalues
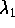 and
and 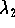 are
negative (with
are
negative (with 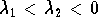 ). When
). When 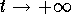 , the solutions "die" at the origin. They tend to
the equilibrium point tangent to the straight-line
solution associated to the eigenvalue
, the solutions "die" at the origin. They tend to
the equilibrium point tangent to the straight-line
solution associated to the eigenvalue 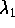 .
.
In this case the equilibrium point is a sink.
-

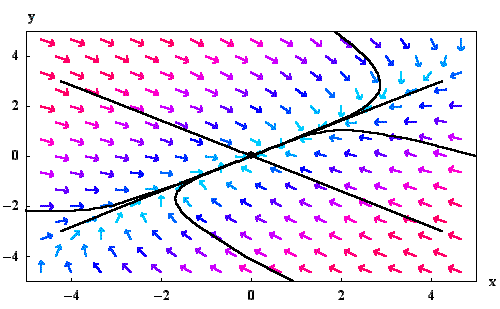
- The two eigenvalues
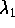 and
and 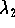 have
different signs (with
have
different signs (with  ). In this case,
the solutions explode whether when
). In this case,
the solutions explode whether when 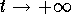 (except
along the straight-line solution associated to the eigenvalue
(except
along the straight-line solution associated to the eigenvalue
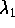 ) or
) or 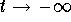 (except along the
straight-line solution associated to the eigenvalue
(except along the
straight-line solution associated to the eigenvalue 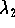 ).
).
In this case, the equilibrium point is a saddle.
-

- Repeated Real nonzero eigenvalue. Let us call
this eigenvalue
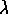 .
We have two cases
.
We have two cases
-

- If
 ,
then the solutions tend either to the
equilibrium point tangent to the only straight-line solution,
,
then the solutions tend either to the
equilibrium point tangent to the only straight-line solution,
or it can happen that all solutions (except for the equilibrium point) are straight-line solutions,
approaching the equilibrium point:
-

- If
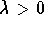 , then the solutions get large as
, then the solutions get large as 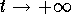 . But even if the solution explodes, it does go
to infinity either tangent to the straight-line solution,
. But even if the solution explodes, it does go
to infinity either tangent to the straight-line solution,
or goes to infinity straight in every direction:
-

- Zero eigenvalue. If the system has zero as an
eigenvalue, then there exists a line of equilibrium points (degenerate
case). Let us call the other eigenvalue
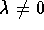 . Note that
the solutions are all straight-line solutions. Depending on the sign
of
. Note that
the solutions are all straight-line solutions. Depending on the sign
of 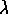 , the solution may tend to or get away from the line of
equilibrium points parallel to the eigenvector associated to the
eigenvalue
, the solution may tend to or get away from the line of
equilibrium points parallel to the eigenvector associated to the
eigenvalue 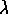 . For a negative
. For a negative 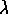 , we have
, we have
and for a positive 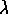 , we have
, we have
-

- Complex eigenvalues. Let us write the
eigenvalues as
 . We have three cases.
. We have three cases.
-

-
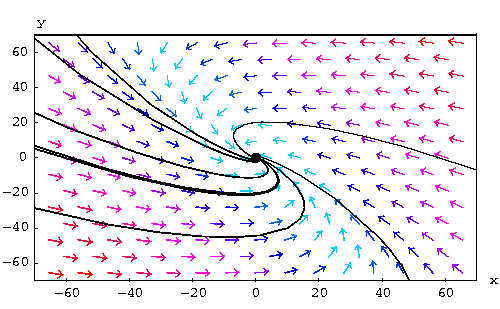
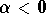 . The
solutions tend to the origin (when
. The
solutions tend to the origin (when 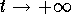 ) while
spiraling. In this case, the equilibrium point is called a
spiral sink.
) while
spiraling. In this case, the equilibrium point is called a
spiral sink.
-

-
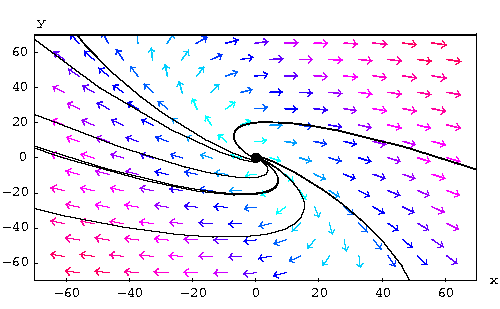
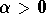 . The
solutions explode or get away from the origin (when
. The
solutions explode or get away from the origin (when 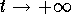 ) while spiraling. In this case, the equilibrium point is
called a spiral source.
) while spiraling. In this case, the equilibrium point is
called a spiral source.
-

-
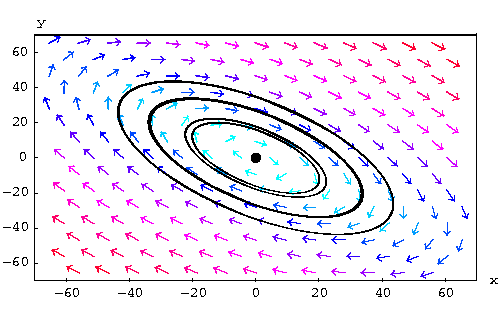
 . The
solutions are periodic. This means that the trajectories are closed
curves or cycles. In this case, the equilibrium point is
called a center.
. The
solutions are periodic. This means that the trajectories are closed
curves or cycles. In this case, the equilibrium point is
called a center.

[Differential Equations]
[First Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Qualitative Analysis of Linear Systems
Qualitative Analysis of Linear Systems Qualitative Analysis of Linear Systems
Qualitative Analysis of Linear Systems
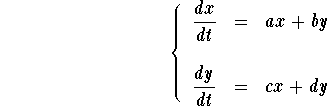
![]()







![]() , we have
, we have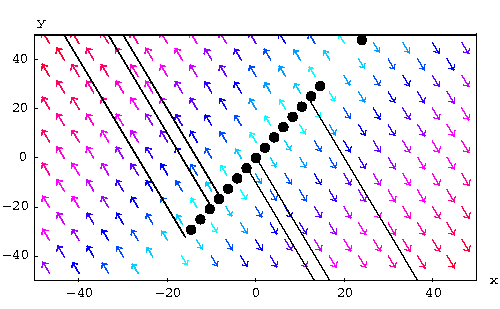

 S.O.S MATHematics home page
S.O.S MATHematics home page 