Second Order Equations and Systems

We have seen before how to solve some type of second order equations. In fact, we have only seen how to solve linear equations. So what happened to nonlinear equations ? Unfortunately many of real life problems are modelled by nonlinear equations. Here we will show how a second order equation may rewritten as a system. The technique developed for the system may then be used to study second order equation even if they are not linear.

Any second order differential equation is given (in the explicit form) as

Let us introduce the function

Then we have

Putting everything together we get

It is very easy to see that y(t) is solution to the second order equation if and only if (y,v) is solution to the system. Keep in mind, that our original problem deals with y(t). Therefore, the phase plane of the system is not as important as if we were only dealing with the associated system. This is another reason why we should also pay attention to the graph of y versus t.

Harmonic Oscillator
The mass-spring apparatus is called the Harmonic oscillator and is one of the most important models in science (specially in physics). This model also rises in circuit theory (RLC circuits) and in physics of particles.
A very rough description of the mass-spring apparatus is:

the mass m of the attached object to the spring;

the spring constant (which is a direct result of Hooke's law);

the coefficient damping which associated to the milieu where the spring-mass live. The damping force may be proportional to the velocity vector or have a very complicated form (not linear at all).

From Newtonian mechanics, we get the differential equation that models the harmonic oscillator

in the absence of an external force acting on the object. Recall that y(t) denotes the position of the object at time t. We are clearly assuming that the motion is linear (that is along a line). Before we write down the associated system, we rewrite the equation in the explicit form

The associated system is

Undamped Harmonic Oscillators
These are harmonic oscillators for which . In this case, the differential equation reduces to

or equivalently

or

The associated system is

Example. Consider the harmonic oscillators

1.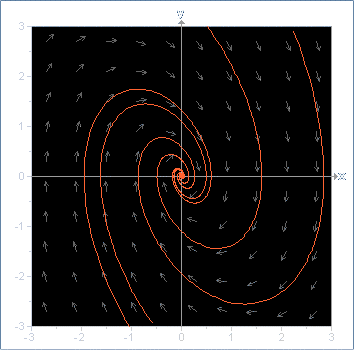

m=1, and ;

2.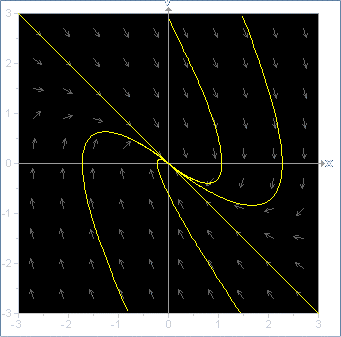

m=1, and ;

3.

m=1, and .

Below we draw their phase planes with some solutions.

1.
2.
3.

[Differential Equations] [First Order D.E.] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

.

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA