 Gibbs Phenomenon
Gibbs Phenomenon

One shortcoming of Fourier series today known as the Gibbs phenomenon was first observed
by H. Wilbraham in 1848 and then analyzed in detail by Josiah W. Gibbs (1839-1903).
We will start with an example.
Example. Consider the function
Since this function is odd, we have an = 0, for 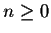 .
A direct calculation gives
.
A direct calculation gives
for 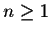 .
The Fourier partial sums of f(x) are
.
The Fourier partial sums of f(x) are
The main Theorem implies that this sequence converges to f(x) except at the point x0 = 0, which a point of discontinuity of f(x). Gibbs got interested to the behavior of the sequence of Fourier partial sums around this point.
Looking at the graphs of the partial sums, we see that a strange phenomenon is happening. Indeed, when x is close to the point 0, the graphs present a bump. Let us do some calculations to justify this phenomenon.
Consider the second derivative of f2n-1, which will help us find the maximum points.
Using trigonometric identities, we get
So the critical points of f2n-1 are
Since the functions are odd, we will only focus on the behavior to the right of 0. The closest critical point to the right of 0 is
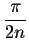 .
Hence
.
Hence
In order to find the asymptotic behavior of the this sequence, when n is large, we will use the Riemann sums. Indeed, consider the function
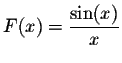 on the interval
on the interval ![$[0,\pi]$](img66.gif) ,
and the partition
,
and the partition
![$\left\{{\displaystyle \frac{k\pi}{n}}, \;\;k \in [1,n]\right\}$](img67.gif) of
of ![$[0,\pi]$](img66.gif) .
So the Riemann sums
.
So the Riemann sums
converges to
 .
Esay calculations show that these sums are equal to
.
Esay calculations show that these sums are equal to
Hence
Using Taylor polynomials of 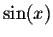 at 0, we get
at 0, we get
i.e. up to two decimals, we have
These bumps seen around 0 are behaving like a wave with a height equal to 0,18. This is not the case only for this function. Indeed, Gibbs showed that if f(x) is piecewise smooth on
![$[-\pi,\pi]$](img27.gif) ,
and x0 is a point of discontinuity, then the Fourier partial sums will exhibit the same behavior, with the bump's height almost equal to
,
and x0 is a point of discontinuity, then the Fourier partial sums will exhibit the same behavior, with the bump's height almost equal to
To smooth this phenomenon, we introduce a new concept called the 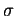 -approximation. Indeed, let
f(x) be a function piecewise smooth on
-approximation. Indeed, let
f(x) be a function piecewise smooth on
![$[-\pi,\pi]$](img27.gif) and fN(x) its Fourier partial sums. Set
and fN(x) its Fourier partial sums. Set
where
which are called the 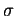 -factors. To see that the sequence of sums
-factors. To see that the sequence of sums
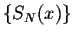 better approximate the function f(x) than the Fourier partial sums
better approximate the function f(x) than the Fourier partial sums
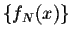 ,
we use the following result:
,
we use the following result:
Theorem. We have
Proof. We have
Similarly, we have
Hence
which yields the conclusion above.
Using the above conclusion, we can easily see that indeed the sums
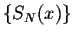 approximate the function f(x) in a very smooth way. On the graphs, we can see that the Gibbs phenomenon has faded away.
approximate the function f(x) in a very smooth way. On the graphs, we can see that the Gibbs phenomenon has faded away.
Example. The picture
shows how the  -approximation helps fade away the Gibbs phenomenon for the function
-approximation helps fade away the Gibbs phenomenon for the function
Note that in this case, we have
and

[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATH: Home Page
S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Gibbs Phenomenon
Gibbs Phenomenon Gibbs Phenomenon
Gibbs Phenomenon
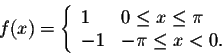


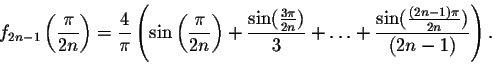
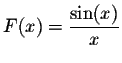 on the interval
on the interval ![$\left\{{\displaystyle \frac{k\pi}{n}}, \;\;k \in [1,n]\right\}$](img67.gif) of
of 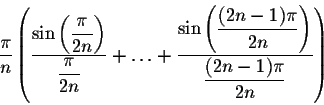
 .
Esay calculations show that these sums are equal to
.
Esay calculations show that these sums are equal to
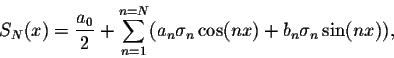


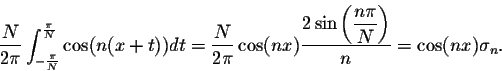
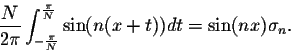
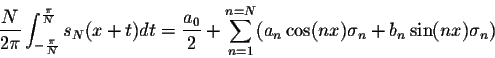
![]() approximate the function f(x) in a very smooth way. On the graphs, we can see that the Gibbs phenomenon has faded away.
approximate the function f(x) in a very smooth way. On the graphs, we can see that the Gibbs phenomenon has faded away.

![]() -approximation helps fade away the Gibbs phenomenon for the function
-approximation helps fade away the Gibbs phenomenon for the function
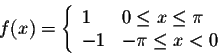
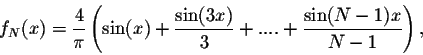
![\begin{displaymath}S_N(x) = \frac{4}{\pi}\left[\sin(x)\sin\left(\frac{\pi}{N}\ri...
...N-1)^2}\sin((N-1)x) \sin\left(\frac{(N-1)\pi}{N}\right)\right].\end{displaymath}](img86.gif)

