 Computation of Eigenvalues
Computation of Eigenvalues

For a square matrix A of order n, the number 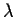 is an eigenvalue if and only if there exists a non-zero vector C such that
is an eigenvalue if and only if there exists a non-zero vector C such that
Using the matrix multiplication properties, we obtain
This is a linear system for which the matrix coefficient is
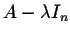 .
We also know that this system has one solution if and only if the matrix coefficient is invertible, i.e.
.
We also know that this system has one solution if and only if the matrix coefficient is invertible, i.e.
 .
Since the zero-vector is a solution and C is not the zero vector, then we must have
.
Since the zero-vector is a solution and C is not the zero vector, then we must have
Example. Consider the matrix
The equation
 translates into
translates into
which is equivalent to the quadratic equation
Solving this equation leads to
In other words, the matrix A has only two eigenvalues.
In general, for a square matrix A of order n, the equation
will give the eigenvalues of A. This equation is called the characteristic equation or characteristic polynomial of A. It is a polynomial function in 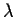 of degree n. So we know that this equation will not have more than n roots or solutions. So a square matrix A of order n will not have more than n eigenvalues.
of degree n. So we know that this equation will not have more than n roots or solutions. So a square matrix A of order n will not have more than n eigenvalues.
Example. Consider the diagonal matrix
Its characteristic polynomial is
So the eigenvalues of D are a, b, c, and d, i.e. the entries on the diagonal.
This result is valid for any diagonal matrix of any size. So depending on the values you have on the diagonal, you may have one eigenvalue, two eigenvalues, or more. Anything is possible.
Remark. It is quite amazing to see that any square matrix A has the same eigenvalues as its transpose AT because
For any square matrix of order 2, A, where
the characteristic polynomial is given by the equation
The number (a+d) is called the trace of A (denoted tr(A)), and clearly the number (ad-bc) is the determinant of A. So the characteristic polynomial of A can be rewritten as
Let us evaluate the matrix
B = A2 - tr(A) A + det(A) I2.
We have
We leave the details to the reader to check that
In other word, we have
This equation is known as the Cayley-Hamilton theorem. It is true for any square matrix A of any order, i.e.
where
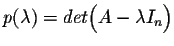 is the characteristic polynomial of A.
is the characteristic polynomial of A.
We have some properties of the eigenvalues of a matrix.
Theorem. Let A be a square matrix of order n. If 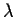 is an eigenvalue of A, then:
is an eigenvalue of A, then:
- 1.
 is an eigenvalue of Am, for
is an eigenvalue of Am, for
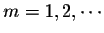
- 2.
- If A is invertible, then
 is an eigenvalue of A-1.
is an eigenvalue of A-1.
- 3.
- A is not invertible if and only if
 is an eigenvalue of A.
is an eigenvalue of A.
- 4.
- If
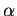 is any number, then
is any number, then
 is an eigenvalue of
is an eigenvalue of
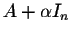 .
.
- 5.
- If A and B are similar, then they have the same characteristic polynomial (which implies they also have the same eigenvalues).
The next natural question to answer deals with the eigenvectors. In the next page, we will discuss the problem of finding eigenvectors..

[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Differential Equations]
[Matrix Algebra]
 S.O.S MATH: Home Page
S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 Computation of Eigenvalues
Computation of Eigenvalues Computation of Eigenvalues
Computation of Eigenvalues
![]() is an eigenvalue if and only if there exists a non-zero vector C such that
is an eigenvalue if and only if there exists a non-zero vector C such that

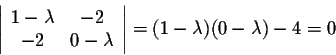



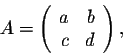
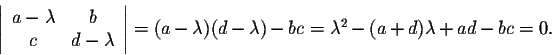

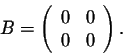
![]() is an eigenvalue of A, then:
is an eigenvalue of A, then:

