Invertible Matrices

Invertible matrices are very important in many areas of science. For example, decrypting a coded message uses invertible matrices (see the coding page). The problem of finding the inverse of a matrix will be discussed in a different page (click here).

Definition. An $n\times n$ matrix A is called nonsingular or invertible iff there exists an $n\times n$ matrix B such that

\begin{displaymath}A\;B = B\; A = I_n\end{displaymath}

where In is the identity matrix. The matrix B is called the inverse matrix of A.

Example. Let

\begin{displaymath}A = \left(\begin{array}{rrr} 2&3\\ 2&2\\ \end{array}\right)... ...left(\begin{array}{rrr} -1&3/2\\ 1&-1\\ \end{array}\right)\;.\end{displaymath}

One may easily check that

\begin{displaymath}A\;B = B\;A = \left(\begin{array}{rrr} 1&0\\ 0&1\\ \end{array}\right) = I_2\;.\end{displaymath}

Hence A is invertible and B is its inverse.

Notation. A common notation for the inverse of a matrix A is A-1. So

\begin{displaymath}A\; A^{-1} = A^{-1}\;A = I_n\;.\end{displaymath}

Example. Find the inverse of

\begin{displaymath}A = \left(\begin{array}{rrr} 1&1\\ -1&2\\ \end{array}\right).\end{displaymath}

Write

\begin{displaymath}A^{-1} = \left(\begin{array}{rrr} a&b\\ c&d\\ \end{array}\right).\end{displaymath}

Since

\begin{displaymath}A\;A^{-1} = \left(\begin{array}{cc} a+c&b+d\\ -a +2c&-b+2d\\ \end{array}\right) = I_2\end{displaymath}

we get

\begin{displaymath}\left\{\begin{array}{ccccc} a &+& c &=& 1\\ -a &+& 2c &=& 0\\ b &+& d &=& 0\\ -b &+& 2d &=& 1\\ \end{array}\right.\end{displaymath}

Easy algebraic manipulations give

\begin{displaymath}a = \frac{2}{3},\;\; b = -\frac{1}{3},\;\; c = \frac{1}{3},\;\; d = \frac{1}{3}\end{displaymath}

or

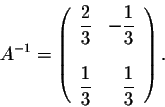
\begin{displaymath}A^{-1} = \left(\begin{array}{rrr} \displaystyle \frac{2}{3}&\... ...le \frac{1}{3}&\displaystyle \frac{1}{3}\\ \end{array}\right).\end{displaymath}

The inverse matrix is unique when it exists. So if A is invertible, then A-1 is also invertible and

\begin{displaymath}\Big(A^{-1}\Big)^{-1} = A\;.\end{displaymath}

The following basic property is very important:

If A and B are invertible matrices, then $A\;B$ is also invertible and

\begin{displaymath}\Big(A\;B\Big)^{-1} = B^{-1}\;A^{-1}\;.\end{displaymath}

Remark. In the definition of an invertible matrix A, we used both $A\;B$ and $B\;A$ to be equal to the identity matrix. In fact, we need only one of the two. In other words, for a matrix A, if there exists a matrix B such that $A\;B = I_n$, then A is invertible and B = A-1.

More on invertible matrices and how to find the inverse matrices will be discussed in the Determinant and Inverse of Matrices page.

[Geometry] [Algebra] [Trigonometry ]
[Calculus] [Differential Equations] [Matrix Algebra]

S.O.S MATH: Home Page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA