 More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices

Problem. Let 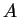 and
and 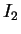 be the matrices
be the matrices
Show that if 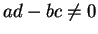 then
then 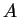 and
and 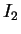 are row equivalent.
are row equivalent.
Recall that two matrices are row equivalent iff one may be obtained from the other one via row elementary operations.
Answer.
If you prefer to jump to the next problem, click on Next Problem
below.

[Next Problem]
[Matrix Algebra]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Calculus]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices
![]() and
and ![]() be the matrices
be the matrices
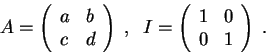

 S.O.S MATHematics home page
S.O.S MATHematics home page 