 More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices

Write 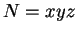 . By definition we have
. By definition we have
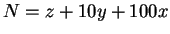 . The first condition translates into
. The first condition translates into
Since the new number with reversed digits is
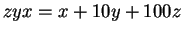 , the second condition translates into
, the second condition translates into
And finally the last condition gives
Putting all the above equations together we get
or
Consider the augmented matrix of this system
Let us do some elementary row operations to solve it. First we
interchange the third row with the first one and multiply the new
first row with 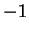 to get
to get
Next take the
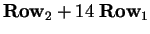 and
and
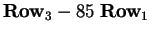 to get
to get
Next take
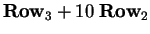 to get
to get
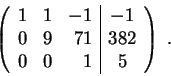
Divide the third row with 781 to get
Next take
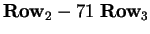 and
and
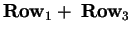 to get
to get
Divide the second row by 9 to get
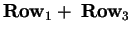 to get
to get
Finally take
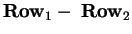 to get
to get
So we have
or 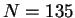 . Check that the original conditions are satisfied.
. Check that the original conditions are satisfied.
Click on Next Problem below to go to the next problem.

[Next Problem]
[Matrix Algebra]
[Trigonometry]
[Calculus]
[Geometry]
[Algebra]
[Differential Equations]
[Calculus]
[Complex Variables]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices More Problems on Linear Systems and Matrices
More Problems on Linear Systems and Matrices
![]() . By definition we have
. By definition we have
![]() . The first condition translates into
. The first condition translates into
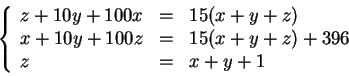
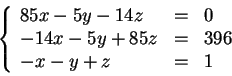
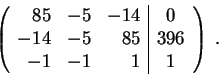
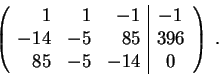
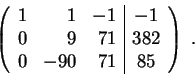
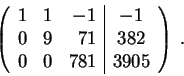
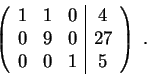
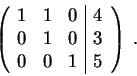
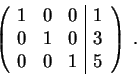

 S.O.S MATHematics home page
S.O.S MATHematics home page 