First and Second Order Differential Equations
First and Second Order Differential Equations
A first order differential equation is of the form:
The general general solution is given by
where
is called the integrating factor.
.
.
is homogeneous if the function f(x,y) is homogeneous, that is
By substitution, we consider the new function
The new differential equation satisfied by z is
which is a separable equation. The solutions are the constant ones f(1,z) - z =0 and the non-constant ones given by
Do not forget to go back to the old function y = xz.
is exact if
The condition of exactness insures the existence of a function F(x,y) such that
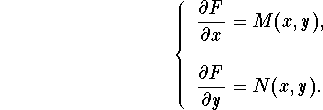
All the solutions are given by the implicit equation
Write down the characteristic equation
and 
are distinct real numbers (this happens
if 
), then the general solution is
(which happens if 
), then the
general solution is
and are complex numbers (which happens if
), then the general solution is
where
that is
The general solution is given by
where 
is a particular solution and 
is the general
solution of the associated homogeneous equation
In order to find 
two major techniques were developed.
where a, b, and c are constant and
where 
is a polynomial function with degree n. In this case, we have
where
The constants 
and 
have to be determined. The power
s is equal to 0 if 
is not a root of the
characteristic equation. If is a simple root, then
s=1 and s=2 if it is a double root.
Remark. If the nonhomogeneous term g(x)
satisfies the following
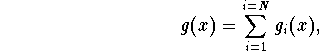
where 
are of the forms cited above, then we split the
original equation into N equations
then find a particular solution 
. A particular solution to the
original equation is given by
of the homogeneous equation
Note that this method works regardless if the coefficients are constant or not. a particular solution as
where 
and 
are functions. From this, the method got its name.
The functions and are solutions to the system:
which implies
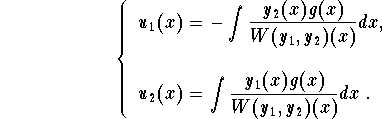
Therefore, we have
where b and c are constant numbers. By substitution, set
then the new equation satisfied by y(t) is
which is a second order differential equation with constant coefficients.
and are distinct real numbers,
then the general solution is given by
and are equal ( ), then
the general solution is
and are complex numbers, then the
general solution is
where 
and 
.
S.O.S MATHematics home page 