 COMMON SUBSTITUTIONS
COMMON SUBSTITUTIONS

- 1.
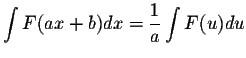
where
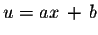
- 2.
-
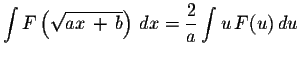
where
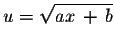
- 3.
-
![$\displaystyle \int F\left( \sqrt[n]{ax+b} \right) \,dx = \displaystyle \frac{n}{a} \displaystyle \int u^{n-1}\,F(u)\,du$](img5.gif)
where
![$u=\sqrt[n]{ax+b}$](img6.gif)
- 4.
-
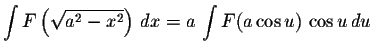
where 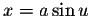
- 5.
-
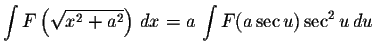
where 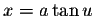
- 6.
-

where 
- 7.
-
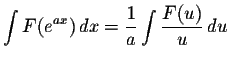
where
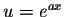
- 8.
-
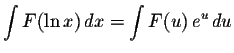
where 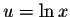
- 9.
-
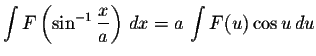
where
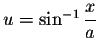

[Tables]
 S.O.S MATHematics home page
S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
 COMMON SUBSTITUTIONS
COMMON SUBSTITUTIONS COMMON SUBSTITUTIONS
COMMON SUBSTITUTIONS
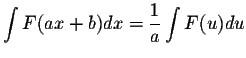
![]()
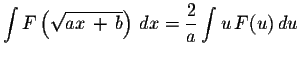
![$\displaystyle \int F\left( \sqrt[n]{ax+b} \right) \,dx = \displaystyle \frac{n}{a} \displaystyle \int u^{n-1}\,F(u)\,du$](img5.gif)
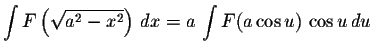
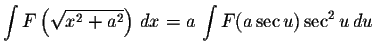

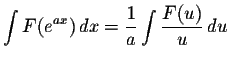
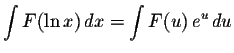
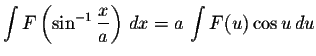
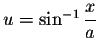

 S.O.S MATHematics home page
S.O.S MATHematics home page 