 INTEGRALS CONTAINING Cosh(ax)
INTEGRALS CONTAINING Cosh(ax) INTEGRALS CONTAINING Cosh(ax)
INTEGRALS CONTAINING Cosh(ax)

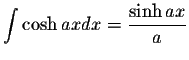
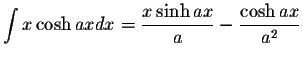
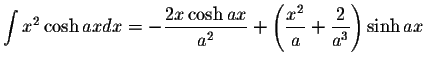
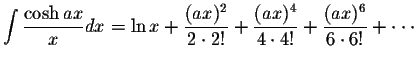
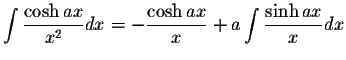
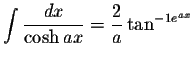
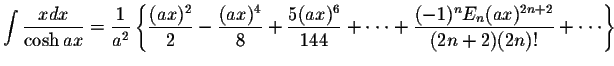
where the constants En are the Euler's numbers.
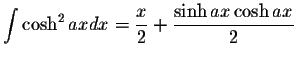
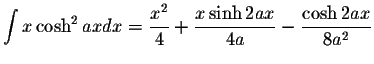
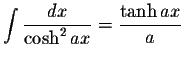
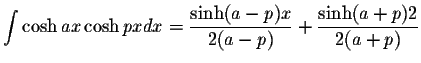
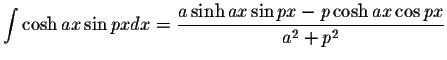
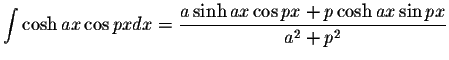
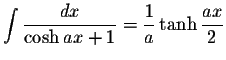
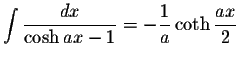
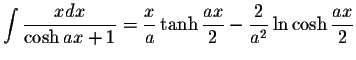
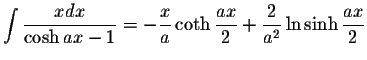
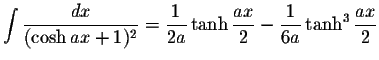
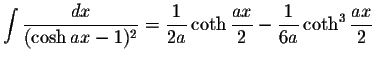
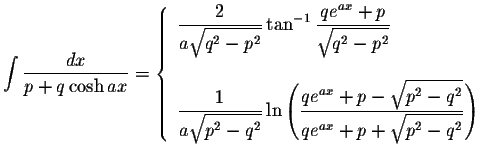
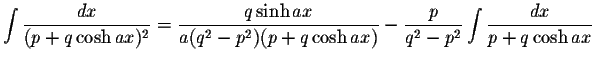
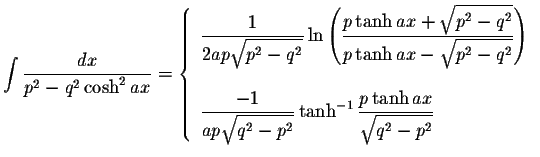
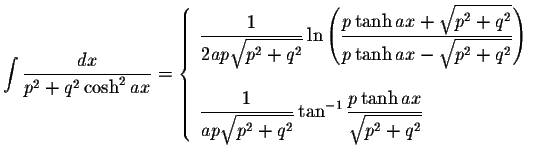
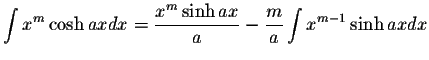
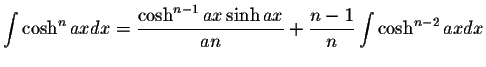
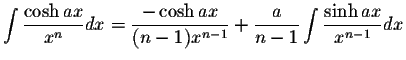
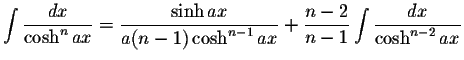
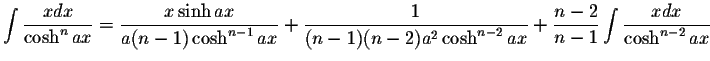

 S.O.S MATHematics home page
S.O.S MATHematics home page 