 INTEGRALS CONTAINING RECIPROCALS OF HYPERBOLIC FUNCTIONS
INTEGRALS CONTAINING RECIPROCALS OF HYPERBOLIC FUNCTIONS INTEGRALS CONTAINING RECIPROCALS OF HYPERBOLIC FUNCTIONS
INTEGRALS CONTAINING RECIPROCALS OF HYPERBOLIC FUNCTIONS



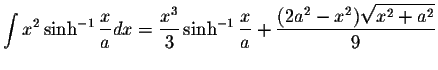

where ![]() is |x| < a,
is |x| < a, ![]() is x>a, and
is x>a, and
![]() is x<-a.
is x<-a.
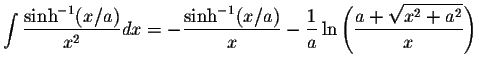
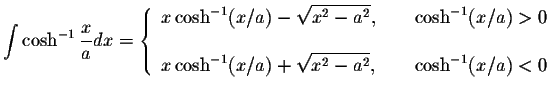

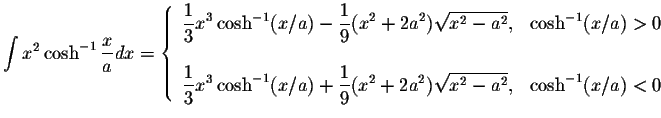
![$\displaystyle\int\displaystyle \frac{\cosh^{-1}(x/a)}{x}dx=\pm\left[\displaysty...
...{1\cdot 3\cdot 5(a/x)^6}{2\cdot 4\cdot 6\cdot 6\cdot 6}+\cdot\cdot\cdot \right]$](img12.gif)

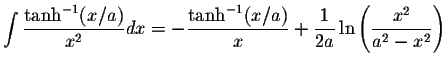
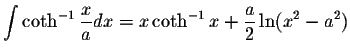
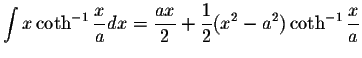

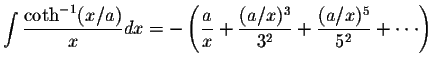
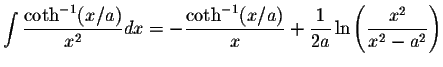
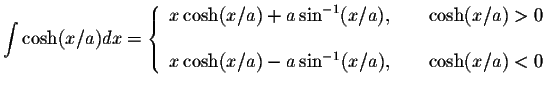
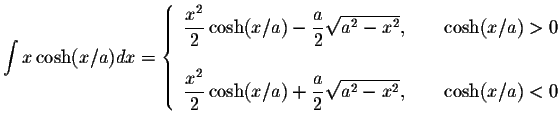
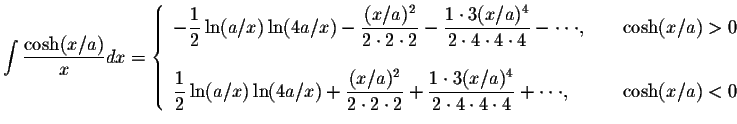

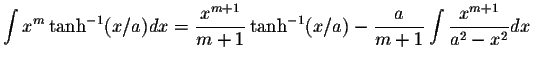
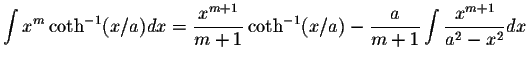
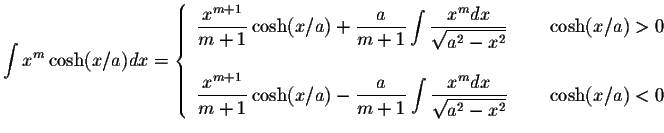
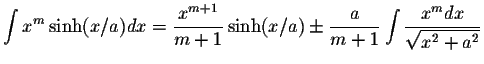

 S.O.S MATHematics home page
S.O.S MATHematics home page 