| = | 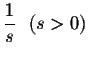 |
(1) | |
| = | 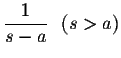 |
(2) | |
| = | 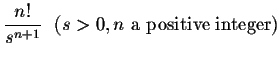 |
(3) | |
| = | 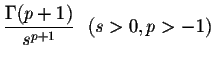 |
(4) | |
| = | 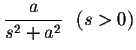 |
(5) | |
| = | 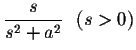 |
(6) | |
| = | 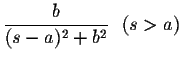 |
(7) | |
| = | 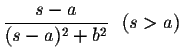 |
(8) | |
| = | 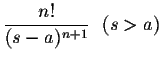 |
(9) | |
| = | 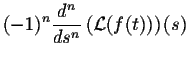 |
(10) | |
| = | (11) | ||
| = | 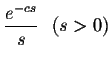 |
(12) | |
| = | (13) | ||
| = | (14) | ||
| = | e-cs | (15) | |
| = | (16) |
| = | 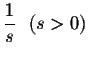 |
(1) | |
| = | 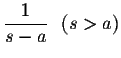 |
(2) | |
| = | 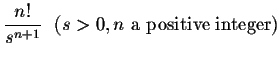 |
(3) | |
| = | 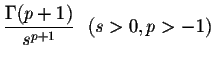 |
(4) | |
| = | 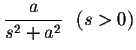 |
(5) | |
| = | 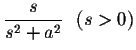 |
(6) | |
| = | 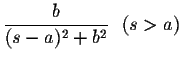 |
(7) | |
| = | 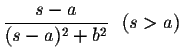 |
(8) | |
| = | 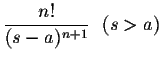 |
(9) | |
| = | 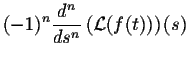 |
(10) | |
| = | (11) | ||
| = | 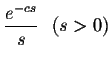 |
(12) | |
| = | (13) | ||
| = | (14) | ||
| = | e-cs | (15) | |
| = | (16) |

 S.O.S MATHematics home page
S.O.S MATHematics home page 
1998-12-04