 Polynomial Long Division
Polynomial Long Division Polynomial Long Division
Polynomial Long Division
In this section you will learn how to rewrite a rational function such as
![]()
in the form
![]()
The expression
![]()
is called the quotient, the expression
![]()
is called the divisor and the term
![]()
is called the remainder.
What is special about the way the expression above is written?
The remainder 28x+30 has degree 1, and is thus less than the degree of the divisor ![]() .
.
It is always possible to rewrite a rational function in this manner:
|
DIVISION ALGORITHM: If f(x) and and so that the degree of r(x) is less than the degree of d(x). In the special case where r(x)=0, we say that d(x) divides evenly into f(x). |
How do you do this? Let's look at our example
![]()
in more detail. Write the expression in a form reminiscent of long division:
![]()
First divide the leading term ![]() of the numerator polynomial by the leading term
of the numerator polynomial by the leading term ![]() of the divisor, and write the answer 3x on the top line:
of the divisor, and write the answer 3x on the top line:
![]()
Now multiply this term 3x by the divisor ![]() , and write the answer
, and write the answer
![]()
under the numerator polynomial, lining up terms of equal degree:
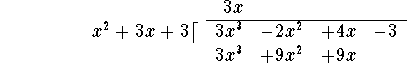
Next subtract the last line from the line above it:
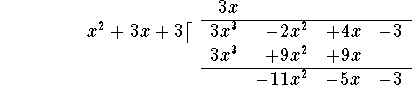
Now repeat the procedure:
Divide the leading term ![]() of the polynomial on the last line by the leading term
of the polynomial on the last line by the leading term ![]() of the divisor to obtain -11, and add this term to the 3x on the top line:
of the divisor to obtain -11, and add this term to the 3x on the top line:
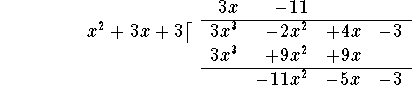
Then multiply "back": ![]() and write the answer
under the last line polynomial, lining up terms of equal degree:
and write the answer
under the last line polynomial, lining up terms of equal degree:
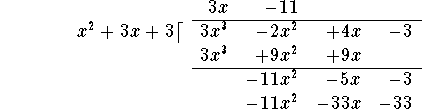
Subtract the last line from the line above it:
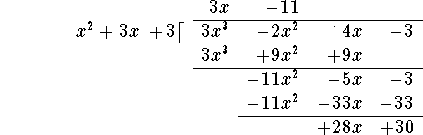
You are done! (In the next step, you would divide 28x by ![]() , not yielding a polynomial expression!)
The remainder is the last line: 28x+30, and the quotient is the expression on the very top: 3x-11. Consequently,
, not yielding a polynomial expression!)
The remainder is the last line: 28x+30, and the quotient is the expression on the very top: 3x-11. Consequently,
![]()
The easiest way to check your answer algebraically is to multiply both sides by the divisor:
![]()
then to multiply out:
![]()
and then to simplify the right side:
![]()
Indeed, both sides are equal! Other ways of checking include graphing both sides (if you have a graphing calculator), or plugging in a few numbers on both sides (this is not always 100% foolproof).
Let's use polynomial long division to rewrite
![]()
Write the expression in a form reminiscent of long division:
![]()
First divide the leading term ![]() of the numerator polynomial by the leading term x of the divisor, and write the answer
of the numerator polynomial by the leading term x of the divisor, and write the answer ![]() on the top line:
on the top line:
![]()
Now multiply this term ![]() by the divisor x+2, and write the answer
by the divisor x+2, and write the answer
![]()
under the numerator polynomial, carefully lining up terms of equal degree:
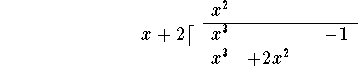
Next subtract the last line from the line above it:
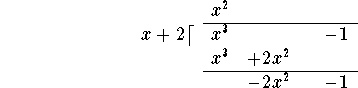
Now repeat the procedure:
Divide the leading term ![]() of the polynomial on the last line by the leading term x
of the divisor to obtain -2x, and add this term to the
of the polynomial on the last line by the leading term x
of the divisor to obtain -2x, and add this term to the ![]() on the top line:
on the top line:
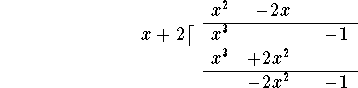
Then multiply "back": ![]() and write the answer
under the last line polynomial, lining up terms of equal degree:
and write the answer
under the last line polynomial, lining up terms of equal degree:
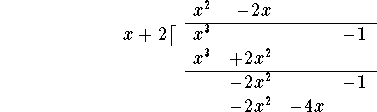
Subtract the last line from the line above it:
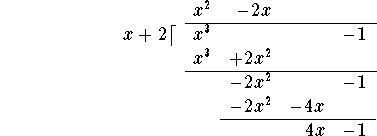
You have to repeat the procedure one more time.
Divide:
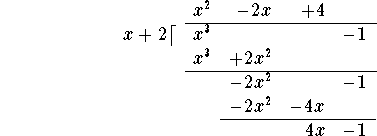
Multiply "back":
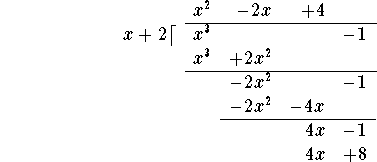
and subtract:
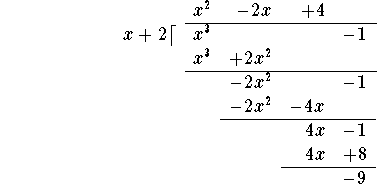
You are done! (In the next step, you would divide -9 by x, not yielding a polynomial expression!)
The remainder is the last line: -9 (of degree 0), and the quotient is the expression on the very top: ![]() . Consequently,
. Consequently,
![]()
Let's use polynomial long division to rewrite
![]()
Write the expression in a form reminiscent of long division:
![]()
First divide the leading term ![]() of the numerator polynomial by the leading term
of the numerator polynomial by the leading term ![]() of the divisor, and write the answer x on the top line:
of the divisor, and write the answer x on the top line:
![]()
Now multiply this term x by the divisor ![]() , and write the answer
, and write the answer
![]()
under the numerator polynomial, carefully lining up terms of equal degree:
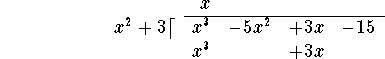
Next subtract the last line from the line above it:
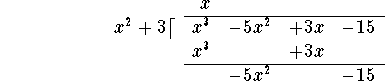
Now repeat the procedure:
Divide the leading term ![]() of the polynomial on the last line by the leading term
of the polynomial on the last line by the leading term ![]() of the divisor to obtain -5, and add this term to the x on the top line:
of the divisor to obtain -5, and add this term to the x on the top line:
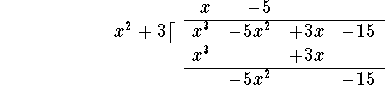
Then multiply "back": ![]() and write the answer
under the last line polynomial, lining up terms of equal degree:
and write the answer
under the last line polynomial, lining up terms of equal degree:
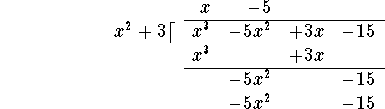
Subtract the last line from the line above it:
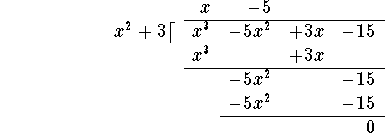
You are done! In this case, the remainder is 0, so ![]() divides evenly into
divides evenly into ![]() .
.
Consequently,
![]()
Multiplying both sides by the divisor ![]() yields:
yields:
![]()
In this case, we have factored the polynomial ![]() , i.e., we have written it as a product of two "easier" (=lower degree) polynomials.
, i.e., we have written it as a product of two "easier" (=lower degree) polynomials.
![]()
![]()
![]()
![]()
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page 
Fri Jun 6 13:11:33 MDT 1997