Factoring and Roots of Polynomials

What is factoring?

If you write a polynomial as the product of two or more polynomials, you have factored the polynomial. Here is an example:

The polynomials x-3 and are called factors of the polynomial . Note that the degrees of the factors, 1 and 2, respectively, add up to the degree 3 of the polynomial we started with. Thus factoring breaks up a complicated polynomial into easier, lower degree pieces.

We are not completely done; we can do better: we can factor

We have now factored the polynomial into three linear (=degree 1) polynomials. Linear polynomials are the easiest polynomials. We can't do any better. Whenever we cannot factor any further, we say we have factored the polynomial completely.

Roots of polynomials.

An intimately related concept is that of a root, also called a zero, of a polynomial. A number x=a is called a root of the polynomial f(x), if

Once again consider the polynomial

Let's plug in x=3 into the polynomial.

Consequently x=3 is a root of the polynomial . Note that (x-3) is a factor of .

Let's plug in into the polynomial:

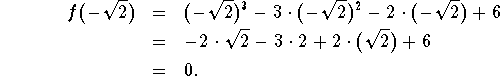
Thus, is a root of the polynomial . Note that is a factor of .

Roots and factoring.

This is no coincidence! When an expression (x-a) is a factor of a polynomial f(x), then f(a)=0.

Since we have already factored

there is an easier way to check that x=3 and are roots of f(x), using the right-hand side:

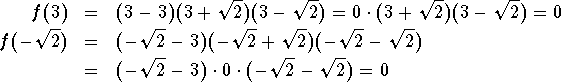
Does this work the other way round? Let's look at an example: consider the polynomial . Note that x=2 is a root of f(x), since

Is (x-2) a factor of ? You bet! We can check this by using long polynomial division:

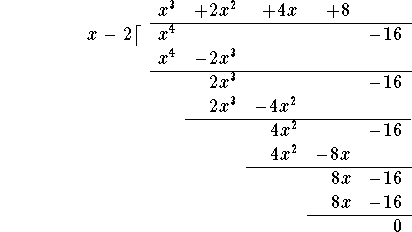
So we can factor

Let's sum up: Finding a root x=a of a polynomial f(x) is the same as having (x-a) as a linear factor of f(x). More precisely:

Given a polynomial f(x) of degree n, and a number a, then

if and only if there is a polynomial q(x) of degree n-1 so that

Exercise 1.

Write down a polynomial with roots x=1, x=2, and x=3/4.

Answer.

Exercise 2.

Write down a polynomial with roots x=-1, x=3, and x=0.

Answer.

Exercise 3.

Factor the polynomial . Note that f(-2)=0.

Answer.

Exercise 4.

Factor the polynomial completely. Note that and .

Answer.

[Back] [Next] [Algebra] [Trigonometry] [Complex Variables] [Calculus] [Differential Equations] [Matrix Algebra]

S.O.S MATHematics home page

Copyright © 1999-2004 MathMedics, LLC. All rights reserved.
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA