Solving Rational Inequalities Analytically

Find the solutions of the inequality

$\begin{displaymath}\frac{x^2+5x+6}{x^2-4x-5}\leq 0.\end{displaymath}$

Since the numerator can be factored as

x²+5x+6=(x+2)(x=3),

while the denominator can be factored as

x²-4x-5=(x+1)(x-5),

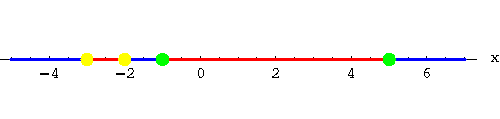
the inequality has four critical points: x=-3, x=-2, x=-1 and x=5:

Consequently, the set of solutions of the inequality is the union of the interval [-3,-2] and the interval (-1,5).

1998-06-16