Solving Polynomial Inequalities Analytically

This section assumes that you know how to find the roots of a polynomial. It also helps if you have visited the warm-up section.

Let's suppose you want to solve the inequality

x²-4x+3<0.

Step 1. Solve the equation f(x)=x²-4x+3=0.

In this case, we can "factor by guessing":

x²-4x+3=(x-1)(x-3),

so the roots of the equation f(x)=0 are x=1 and x=3. Draw a picture of the x-axis and mark these points.

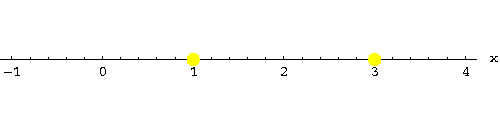
Step 2. Our solutions partition the x-axis into three intervals. Pick a point (your choice!) in each interval. Let me take x=0,x=2 and x=4. Compute f(x) for these points:

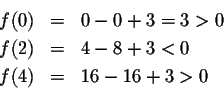
$\begin{eqnarray*}f(0)&=&0-0+3=3>0\\ f(2)&=&4-8+3<0\\ f(4)&=&16-16+3>0 \end{eqnarray*}$

These three points are representative for what happens in the intervals they are contained in:

Since f(0)>0, f(x) will be positive for all x in the interval $(-\infty,1)$ . Similarly, since f(2)<0, f(x) will be negative for all x in the interval (1,3). Since f(4)>0, f(x) will be positive for all x in the interval $(3,\infty)$ . You can indicate this on the x-axis by inserting plus or minus signs on the x-axis. I use color coding instead: blue for positive, red for negative:

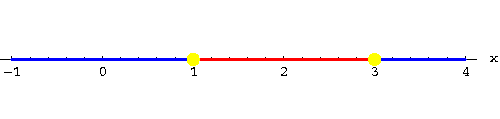
Step 3. We want to solve the inequality

x²-4x+3<0,

so we are looking for all x such that f(x)<0. Consequently, the interval (1,3) contains all solutions to the inequality.

Why does this work? Let's look at the graph of f(x):

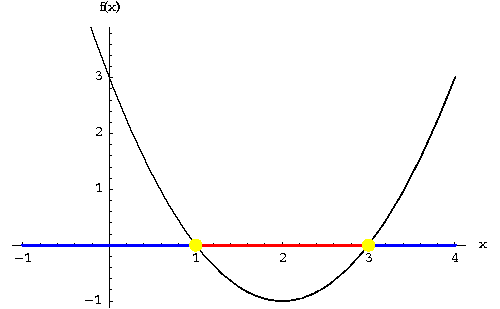
Note the pivotal role played by the "yellow dots", the x-intercepts of f(x).

f(x) can only change its sign by passing through an x-intercept, i.e., a solution of f(x)=0 will always separate parts of the graph of f(x) above the x-axis from parts below the x-axis. Thus it suffices to pick a representative in each of the three intervals separated by "yellow dots", to test whether f(x) is positive or negative in the interval .

This nice property of polynomials is called the Intermediate Value Property of polynomials; your teacher might also refer to this property as continuity.

Here is another example: Find the solutions of the inequality

$\begin{displaymath}x^2+2\geq 3x.\end{displaymath}$

For our method to work it is essential that the right side of the inequality equals zero! So let's change our inequality to

$\begin{displaymath}x^2-3x+2\geq 0.\end{displaymath}$

Step 1. Solve the equation f(x)=x²-3x+2=0.

Again, we can "factor by guessing":

x²-3x+2=(x-1)(x-2),

so the roots of the equation f(x)=0 are x=1 and x=2. Draw a picture of the x-axis and mark these points.

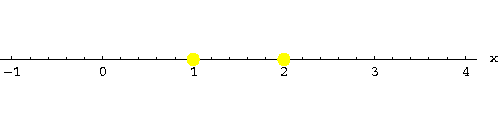
Step 2. Our solutions partition the x-axis into three intervals. Pick a point (your choice!) in each interval. Let me take x=0,x=1.5 and x=3. Compute f(x) for these points:

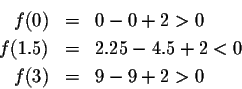
$\begin{eqnarray*}f(0)&=&0-0+2>0\\ f(1.5)&=&2.25-4.5+2<0\\ f(3)&=&9-9+2>0 \end{eqnarray*}$

These three points are representative for what happens in the intervals they are contained in:

Since f(0)>0, f(x) will be positive for all x in the interval $(-\infty,1)$ . Similarly, since f(1.5)<0, f(x) will be negative for all x in the interval (1,2). Since f(3)>0, f(x) will be positive for all x in the interval $(2,\infty)$ . You can indicate this on the x-axis by inserting plus or minus signs on the x-axis. I use color coding instead: blue for positive, red for negative:

Step 3. We want to solve the inequality

$\begin{displaymath}x^2-3x+2\geq 0,\end{displaymath}$

so we are looking for all x such that $f(x)\geq 0$ . Consequently, the set $(-\infty,1]\cup [2,\infty)$ contains all solutions to the inequality. (Since our inequality only stipulates that $f(x)\geq 0$ , x=1 and x=2 are solutions, so we include them. " $+\infty$ " and " $-\infty$ " are only symbols; they will never be included as solutions.)

Our next example: Solve x³>2x. Do not divide by x on both sides! If you do so, you will never be able to arrive at the correct answer. Repeat the pattern instead; make one side of the inequality equal zero:

x³-2x>0.

Step 1. Solve the equation f(x)=x³-2x=0.

We can factor rather easily:

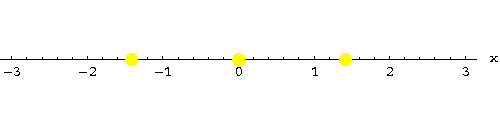
$\begin{displaymath}x^3-2x=x(x^2-2)=x(x-\sqrt{2})(x+\sqrt{2}),\end{displaymath}$

so the roots of the equation f(x)=0 are $x=-\sqrt{2}$ , x=0 and $x=\sqrt{2}$ . Draw a picture of the x-axis and mark these points.

Step 2. Our solutions partition the x-axis into four intervals. Pick a point (your choice!) in each interval. Let me take x=-2,x=-1, x=1 and x=2. Compute f(x) for these points:

$\begin{eqnarray*}f(-2)&=&-8+4<0\\ f(-1)&=&-1+2>0\\ f(1)&=&1-2<0\\ f(2)&=&8-4>0 \end{eqnarray*}$

These four points are representative for what happens in the intervals they are contained in:

Since f(-2)<0, f(x) will be negative for all x in the interval $(-\infty,-\sqrt{2})$ . Similarly, since f(-1)>0, f(x) will be positive for all x in the interval $(-\sqrt{2},0)$ . Since f(1)<0, f(x) will be negative for all x in the interval $(0,\sqrt{2})$ . Since f(2)>0, f(x) will be positive for all x in the interval $(\sqrt{2},\infty)$ . You can indicate this on the x-axis by inserting plus or minus signs on the x-axis. I use color coding instead: blue for positive, red for negative:

Step 3. We want to solve the inequality

x³-2x> 0,

so we are looking for all x such that f(x)> 0. Consequently, the set $(-\sqrt{2},0)\cup (\sqrt{2},\infty)$ contains all solutions to the inequality. (Since our inequality stipulates that f(x)>0, $x=\pm\sqrt{2}$ do not qualify as solutions, so we exclude them. " $+\infty$ " and " $-\infty$ " are only symbols; they will never be included as solutions.)

Here is my last example: Solve

$\begin{displaymath}x^3+3x^2+x+3\leq 0.\end{displaymath}$

Step 1. Solve the equation f(x)=x³+3x²+x+3.

We can factor either by finding a rational zero, or by clever grouping:

x³+3x²+x+3=(x³+3x²)+(x+3)=x²(x+3)+1 (x+3)=(x²+1)(x+3),

so there is only one real root of the equation f(x)=0, namely x=-3. Draw a picture of the x-axis and mark this point.

The polynomial x²+1 is irreducible, it does not have real roots. Its complex roots are irrelevant for our purposes.

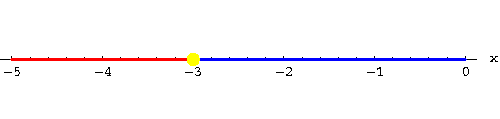
Step 2. Our solution partitions the x-axis into two intervals. Pick a point (your choice!) in each interval. Let me take x=-4 and x=0. Compute f(x) for these points:

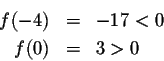
$\begin{eqnarray*}f(-4)&=&-17<0\\ f(0)&=&3>0 \end{eqnarray*}$

These two points are representative for what happens in the intervals they are contained in:

Since f(-4)<0, f(x) will be negative for all x in the interval $(-\infty,-3)$ . Similarly, since f(0)>0, f(x) will be positive for all x in the interval $(-3,\infty)$ . You can indicate this on the x-axis by inserting plus or minus signs on the x-axis. I use color coding instead: blue for positive, red for negative:

Step 3. We want to solve the inequality

$\begin{displaymath}x^3+3x^2+x+3\leq 0,\end{displaymath}$

so we are looking for all x such that $f(x)\leq 0$ . Consequently, the set $(-\infty,-3]$ is the set of solutions to the inequality. (Since our inequality stipulates that $f(x)\leq 0$ , x=-3 is also a solution, so we include it. " $+\infty$ " and " $-\infty$ " are only symbols; they will never be included as solutions.)

Time for you to try it yourself: