 RULES OF LOGARITHMS - Problem 5
RULES OF LOGARITHMS - Problem 5
 RULES OF LOGARITHMS - Problem 5
RULES OF LOGARITHMS - Problem 5 
Let a be a positive number such that a does not equal 1, let
n be a real number, and let u and v be positive real numbers.
Logarithmic Rule 2:
![]()

Problem 5: Simplify 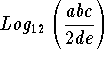 and write the answer in terms of a base 10. What assumptions must be made about a, b, d, and d before you can work this problem?
and write the answer in terms of a base 10. What assumptions must be made about a, b, d, and d before you can work this problem?
Solution: To work the problem as it is, the value of the expression
 must be greater than zero.
must be greater than zero.
The expression 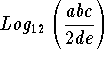 can be simplified to
can be simplified to
![]()
as long as the value of the expressions abc and 2de are both positive.
The expression ![]() can be written as
can be written as
![]()
as long as a, b, c, d, and e are all positive.
If the values of a, b, c, d, and e are all positive, then we can expand the original expression to the last expression. If the values are not all positive, then we cannot expand the original expression.
![]()
can be written in terms of base 10 as
![]()
Check: Since 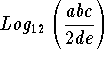 is equivalent to
is equivalent to
![]()
let us choose values for a, b, c, d, and e and substitute them into the
original expression and in our final expression, the answers should be
equal. Let us try it.
Suppose a = 2, b = 3, c = 4, d = 5, and e = 6, the original expression has a value
![]()
Now let's substitute these same values in the final expression.
![]()
Both answers are the same, therefore the original expression is equivalent to the final expression as long as a, b, c, d, and e are all positive numbers.
A last check using our numbers:
![]()

 S.O.S.
MATHematics home page
S.O.S.
MATHematics home page