RULES OF LOGARITHMS - Rule 2
RULES OF LOGARITHMS - Rule 2
Let a be a positive number such that a does not equal 1, let n be a real number, and let u and v be positive real numbers.
Logarithmic Rule 2: 
Example 1: Suppose that a base is 6 and exponents are 10 and 3. We could solve the exponential problem 
by calculating 
and
and dividing the results. 
, 
and their quotient is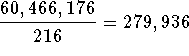 
. You could also solve the problem by first combining the exponents
The same is true of logarithms. Suppose you wanted to calculate
You could calculate the answer by first dividing 60,466,176 by 216, changing the base of 6 to either 10 or e and calculating the results.
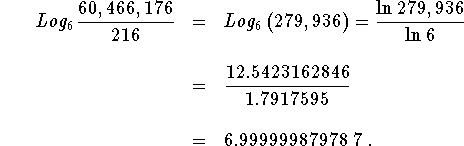
Or you could first combine the logarithms using Rule 2 and then change the bases.
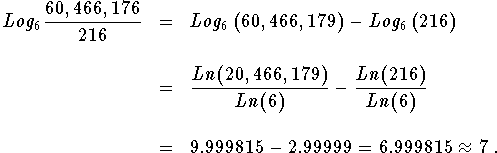
Example 2: Calculate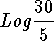 
.
Solution: Note that
Using Rule 2 you could also work the problem by separating .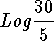
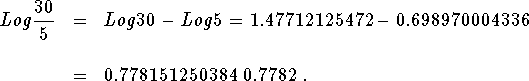
If you would like to review another example, click on Example.
Work the following problems. If you would like to review the answers and solutions, click on answer.
Problem 1: Calculate 
.
Problem 2: Calculate 
.
Problem 3: Calculate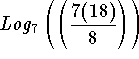 
.
Problem 4: Calculate 
.
Problem 5: Simplify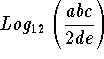 
and write the answer in terms of a base 10. What assumptions must be made about a, b, d, and d before you can work this problem?
S.O.S MATHematics home page