EXPONENTIAL FUNCTIONS

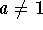The exponential function f with base a is denoted by , where , and x is any real number. The function value will be positive because a positive base raised to any power is positive. This means that the graph of the exponential function will be located in quadrants I and II.

For example, if the base is 2 and x = 4, the function value f(4) will equal 16. A corresponding point on the graph of would be (4, 16).

Definition of Logarithmic Function

For x >0, a>0 , and 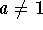, we have

Since x > 0, the graph of the above function will be in quadrants I and IV.

Comments on Logarithmic Functions

The exponential equation could be written in terms of a logarithmic equation as .
The exponential equation can be written as the logarithmic equation .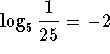
Since logarithms are nothing more than exponents, you can use the rules of exponents with logarithms.
Logarithmic functions are the inverse of exponential functions. For example if (4, 16) is a point on the graph of an exponential function, then (16, 4) would be the corresponding point on the graph of the inverse logarithmic function.
The two most common logarithms are called common logarithms and natural logarithms. Common logarithms have a base of 10, and natural logarithms have a base of e.

If you are interested in reviewing any of the following topics, click the appropriate item:

: The properties of logarithms along with examples and problems, click on Properties

The graphs of logarithms, with examples and problems, click on Graphs of Logarithms

Change of base with respect to logarithms with examples and problems, click on Change of base

The three rules of logarithms, with examples and problems, click on Rules of Logarithms

Solving exponential and logarithms equations with examples and problems, click on Solving Equations

Solving word problems involving exponential and logarithms functions with examples and problems, click on Solving Word Problems
: The graphs of logarithms, with examples and problems, click on Graphs of Logarithms

Change of base with respect to logarithms with examples and problems, click on Change of base

The three rules of logarithms, with examples and problems, click on Rules of Logarithms

Solving exponential and logarithms equations with examples and problems, click on Solving Equations

Solving word problems involving exponential and logarithms functions with examples and problems, click on Solving Word Problems
: Change of base with respect to logarithms with examples and problems, click on Change of base

The three rules of logarithms, with examples and problems, click on Rules of Logarithms

Solving exponential and logarithms equations with examples and problems, click on Solving Equations

Solving word problems involving exponential and logarithms functions with examples and problems, click on Solving Word Problems
: The three rules of logarithms, with examples and problems, click on Rules of Logarithms

Solving exponential and logarithms equations with examples and problems, click on Solving Equations

Solving word problems involving exponential and logarithms functions with examples and problems, click on Solving Word Problems
: Solving exponential and logarithms equations with examples and problems, click on Solving Equations

Solving word problems involving exponential and logarithms functions with examples and problems, click on Solving Word Problems
: Solving word problems involving exponential and logarithms functions with examples and problems, click on Solving Word Problems

[Exponential Rules] [Logarithms]

[Algebra] [Trigonometry ] [Complex Variables]

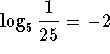S.O.S MATHematics home page